| На главную |
| Структура программы |
| Презентация |
| Статьи |
| Контакты |
|
|

Обязательна ссылка на источник при использовании данных материалов
|
Алейников С. М., Вахтин А. А. Гранично-элементная дискретизация плоских областей в пространстве. // мат. рег. науч.-мет. конф. Информатика: проблемы, методология, технологии. - Воронеж: ВГУ, 2004. - Вып. 4. - С. 6 - 9. |
| Назад |
|
Гранично-элементная дискретизация плоских областей в пространстве Алейников С. М.,
Вахтин А. А. e-mail:
alasmbkb@box.vsi.ru, wishmaster_79@mail.ru Воронежский государственный
архитектурно-строительный университет Воронежский государственный
университет В работе [1] рассмотрен
предпроцессор гранично-элементного программного комплекса, который разработан с
возможностью модификации при расширении диапазона задач в теории упругости
путем добавления новых утилит проектирования. Утилиты проектирования предназначены
для геометрического моделирования сложной поверхности расчитываемой
конструкции, которая разбивается на гранично-элементную сетку.
Гранично-элементная сетка в общем случае представляет собой набор плоских элементов
(как правило, четырехугольных и/или треугольных), не имеющих пересечений и
перекрытий и полностью покрывающих контактную поверхность конструкции. Существующие и
разрабатываемые утилиты можно разбить на два типа: 1)
утилиты генерации гранично-элементной сетки – утилиты, которые
моделируют с заданными параметрами сетку на поверхностях конструкций (например,
утилиты генерации гранично-элементной сетки на поверхностях осесимметричных и
блочных конструкций [1, 2]); 2)
утилиты редактирования гранично-элементной сетки – утилиты, которые
предназначены для редактирования созданной гранично-элементной сетки в
диалоговом и интерактивном режиме (например, утилита «редактор многогранников»,
которая предназначена для добавления, удаления или изменения координат вершин
(узлов) геометрического объекта [3]). Минимальный радиус
окружности описанной вокруг граничного элемента будем называть радиусом граничного
элемента. Часто при решении контактных задач методом граничных элементов
требуется дискретизация поверхности на элементы с малыми радиусами, что характеризует
неравномерность сетки [4]. В некоторых утилитах неравномерность сетки
задается в процессе проектирования. Но в основном требуется разбиение элементов
не всей поверхности, а определенной области (например, в близи углов и ребер
расчитываемой конструкции). Элемент гранично-элементной
сетки, который требуется разбить на элементы меньшего радиуса, будем называть граничным
макроэлементом, а элементы, полученные в результате дискретизации макроэлемента
– микроэлементами [4]. Разбиение четырехугольного граничного макроэлемента
производится с помощью изопараметрических элементов. Описание геометрии в
плоскости данного макроэлемента получается с использованием интерполяционных формул
[4]. Если на стандартном квадрате берется равномерная или сгущающаяся к границе
сетка элементов, то линейное изопараметрическое преобразование переведет их в
глобальные граничные элементы без нарушения межэлементной непрерывности и с
требуемой регулярной нумерацией узлов и вершин. Интерполяционные формулы для
дискретизации треугольных граничных макроэлементов могут быть получены из
интерполяционных формул дискретизации четырехугольных с учетом того, что две
смежные вершины сливаются в одну. В результате формируется алгоритм
дискретизации треугольных граничных макроэлементов, который весьма просто
позволяет добиваться необходимой степени густоты гранично-элементной сетки. При
разбиении треугольных макроэлементов в качестве вершины сгущения не
рекомендуется брать острые углы, так как при дискретизации может появиться
большое количество микроэлементов с общей вершиной, площадь которых близка к
нулю. Основная задача при дискретизации произвольного односвязного макроэлемента в пространстве – это разбить макроэлемент на четырехугольные и треугольные макроэлементы, которые, в свою очередь, разбиваются на микроэлементы по алгоритмам, описанным выше. Разбиение макроэлемента на треугольные и четырехугольные элементы основан на алгоритме, предложенным в [5]. Идея заключается в расщеплении плоского макроэлемента вдоль некоторой хорды, а затем в рекурсивном разбиении получившихся двух макроэлементов. На основе предложенных
алгоритмов реализована утилита разбиения выделенных элементов
гранично-элементной сетки. Разбиваемые граничные макроэлементы можно выделить в
окнах проекции с помощью мыши или задать в пространстве охватывающую область.
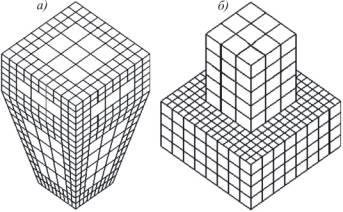
На рис. 1 показаны результаты гранично-элементной дискретизации. Практический опыт
показывает, что разработанная утилита является эффективным средством
корректировки и улучшения гранично-элементных сеток. Возможность генерации
сгущающихся сеток эффективно для оценки точности численного решения.
Рис. 1.
Примеры неравномерной гранично-элементной Литература [1] Вахтин А. А.
Программный пакет автоматизированного твердотельного проектирования. //
Информатика: проблемы, методология, технологии: Матер. 3 регион. науч.-мет.
конф. – Воронеж: ВГУ, 2003. – С. 29-32. [2]
Вахтин А. А., Алейников С. М. Генерация
пространственных гранично-элементных сеток для фундаментных конструкций
блочного типа.// Тр. 4-й междун. Конф. молодых ученых и студентов «Актуальные
проблемы современной науки». Естественные науки. – Ч. 17. Информатика.
Вычислительная техника и управление. – Самара: [3] Вахтин А. А.
Алгоритмы автоматического моделирования
многогранников.// Математическое обеспечение ЭВМ./ Межвуз. сб. науч. тр. – Вып.
4. – Воронеж: ВГУ, 2002. – С. 27 – 31. [4]
Алейников С. М. Метод граничных элементов в контактных
задачах для упругих пространственно неоднородных оснований. – М.: Изд-во «АСВ»,
2000. – 754 с. [5]
Ласло М. Вычислительная геометрия и
компьютерная графика на С++. М.: Из-во БИНОМ, 1997. – 304 с. |