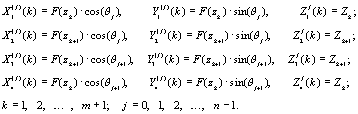ГЕНЕРАЦИЯ ГРАНИЧНО-ЭЛЕМЕНТНОЙ СЕТКИ НА ПОВЕРХНОСТЯХ ОСЕСИММЕТРИЧНЫХ ФУНДАМЕНТОВ

 

Вахтин А. А.

 

Воронежский государственный университет, ф-т ФКН, каф. ПиИТ,

Россия, 394000, г. Воронеж, Университетская пл., 1,

Тел.: (0732) 208-470, e-mail: wishmaster_79@mail.ru

 

 

В строительстве одной из ответственных работ, требующих больших материальных затрат, является расчет и проектирование оснований и фундаментов. От качества фундамента зависит прочность и износостойкость сооружения, что требует проводить тщательные инженерно-изыскательские работы и решение ряда задач геотехники и строительной механики. На практике часто используются осесимметричные фундаменты, в виду простоты геометрического строения конструкций [3].

Несмотря на то, что некоторые фундаментные конструкции изучены (составлены СНИПы и ГОСТы), некоторые задачи остаются открытыми, так как упрощенные формулы механики грунтов, основанные на аналитических решениях простейших задач, не обеспечивают надежности в процессах проектирования, а лабораторный эксперимент сложный, длительный и дорогой.

Поэтому весьма важна роль вычислительного эксперимента в современном геотехническом проектировании, что обусловило появление новой области знания – вычислительной геотехники. Цель вычислительной геотехники – моделирование напряженно-деформированных состояний грунтовых оснований и фундаментов посредством численного решения уравнений математической физики.

Существует два основных численных метода в геотехнических расчетах: метод конечных элементов (МКЭ) и метод граничных элементов (МГЭ). В МКЭ бесконечная область грунтового основания заменяется конечной, однако трудоемкость решения трехмерных задач существенно возрастает. По сравнению с МКЭ, применение МГЭ упрощает подготовку исходных данных, сокращает затраты счетного времени и памяти ЭВМ (в виду то, что свободная поверхность оснований не нуждается в дискретизации на граничные элементы). Благодаря своей наглядности и индифферентности к геометрии МГЭ является в настоящее время наиболее эффективным численным методом для решения пространственных контактных задач в геотехнике [1].

В данной работе рассмотрена утилита генерации гранично-элементной сетки на осесимметричных фундаментных конструкциях к программному модулю URAN [2].

Необходимым условием к разбиению поверхностей фундаментных конструкций на граничные элементы является отсутствие пересечений и перекрытий, а точки на сложной поверхности должны быть узлами смежных граничных элементов. Разбиение в общем случае предполагается смешанным, то есть с одновременным присутствием треугольных и четырехугольных граничных элементов. Локальная нумерация узлов на каждом элементе берется против часовой стрелки при наблюдении со стороны внешней к контактной поверхности нормали (то есть со стороны грунта).

Для всех типов поверхностей принята фрагментальная дискретизация, что соответствует предварительному разбиению поверхности фундаментной конструкции на граничные макроэлементы [1], которые разбиваются на отдельные граничные элементы с автоматической генерацией координат и узлов. В качестве граничных макроэлементов принимаются поверхностные фрагменты, имеющие простейшую топологию. В нашем случае, это кольца, круги, части цилиндрических, конических и сферических поверхностей.

Разбиение граничных макроэлементов на отдельные граничные элементы производится регулярно и не обязательно равномерно.

Важным аспектом фрагментальной дискретизации является согласование по числу граничных элементов на линиях сопряжения сложных граничных макроэлементов. Это необходимо для улучшения численного решения и удобства при обработке и интерпретации полученных результатов.

Осесимметричная поверхность получается в результате вращения некоторой кривой вокруг оси симметрии. Полагаем, что осью симметрии является ось OZ. Тогда уравнение поверхности в цилиндрической системе координат имеет вид

 

      .

 

Для нанесения сетки граничных элементов на поверхность вращения отрезок  делим на m не обязательно равных частей точками

Интервал  изменения угловой координаты q разбиваем на n равных частей плоскостями  (j=0, 1, …, n-1). Рассматривая каждые два последовательных меридиональных сечения    формируем плоские граничные элементы путем вычисления координат вершин по формулам

 

Следует заметить, что в случае, когда F(z)=0 (концевая точка фундаментной конструкции), вторая и третья вершины у граничных элементов сливаются в одну и четырехугольные элементы вырождаются в треугольные. Общее количество плоских граничных элементов на рассмотренном теле вращения будет равно  и растет с увеличением числа разбиений как по глубине (m), так и по угловой координате (n).

В соответствии с принятой терминологией аппроксимируемый фрагмент поверхности вращения с использованием плоских четырехугольных и треугольных граничных элементов будет представлять собой граничный макроэлемент на теле вращения. Разработаны процедуры автоматической дискретизации граничных макроэлементов для наиболее часто встречающихся фрагментов поверхностей вращения

 

цилиндрической:

конической:

сферической:

 

где R – радиус цилиндра или сферы;  – радиусы верхнего и нижнего оснований усеченного конуса соответственно;  – аппликата центра сферы.

Для случаев, когда поверхность тела вращения задается с помощью уравнения вида

применяется еще один, достаточно эффективный способ дискретизации макроэлементов, более удобный, чем рассмотренный выше.

Используем тот факт, что любой фрагмент поверхности вращения, заключенный между плоскостями  и , всегда имеет своей проекцией в плоскости XOY круг или кольцо. Тогда, имея дискретизацию этих плоских канонических областей и применяя указанную выше функциональную зависимость, легко осуществляется аппроксимация граничных макроэлементов на телах вращения плоскими граничными элементами треугольного или четырехугольного типов с непосредственным выполнением требований межэлементной непрерывности. В разработанных процедурах для рассмотренного способа разбиения граничных макроэлементов на плоскости, конической и сферической поверхности использовались регулярные равномерные и неравномерные сетки на круге и кольце, позволяющие получать пространственную дискретизацию нужного качества.

Полная дискретизация поверхности фундаментной конструкции в виде тела вращения получается в результате объединения граничных макроэлементов рассмотренных простейших форм. Когда общее число плоских граничных элементов достаточно велико, а размеры их достаточно малы, то исходя из физических представлений, естественно ожидать, что контактное взаимодействие с грунтом такой фундаментной конструкции (после аппроксимации поверхности ансамблем плоских граничных элементов) под действием внешней нагрузки будет немного отличаться от поведения реального фундамента и что приближенное решение контактной задачи будет сходиться к точному при увеличении числа плоских граничных элементов и уменьшении их размеров. 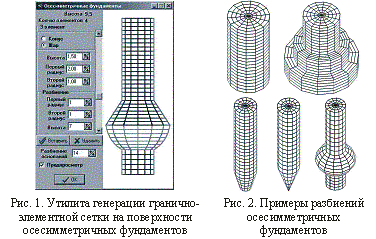Практические расчеты показывают, что имеет место достаточно хорошая сходимость [1].

На основе данных алгоритмов разработанная утилита автоматизированной генерации гранично-элементной сетки на поверхностях осесимметричных фундаментов. Осесимметричные фундаментные конструкции, состоят из набора элементов, боковая поверхность которых имеет цилиндрическую, коническую или сферическую форму, а в основаниях – круговой макроэлемент (рис. 1).

На рис. 2 представлены результаты разбиений для некоторых фундаментных конструкций.

 

 

Разработанные алгоритмы гранично-элементной дискретизации поверхностей осесимметричных фундаментных конструкций характеризуются простой логической структурой и небольшим временем работы ЭВМ. Предложенное конструирование сеточных аппроксимаций позволяет многократно автоматически перестраивать сетки, адаптируя их с помощью локальных сгущений к искомому решению.

 

Литература.

1.        Алейников С. М. Метод граничных элементов в контактных задачах для упругих пространственно неоднородных оснований. – М.: Изд-во «АСВ», 2000. – 754 с.

2.        Вахтин А. А. Программный пакет автоматизированного твердотельного проектирования // Информатика: проблемы, методология, технологии: Матер. 3 регион. науч.-мет. конф. – Воронеж: ВГУ, 2003. – С. 29-32.

3.        Зарецкий Ю. К., Карабаев М. И. Расчет буронабивных свай по определенным состояниям // Основания, фундаменты и механики грунтов. – 1985/ – № 5. – С. 12 – 16.