| На главную |
| Структура программы |
| Презентация |
| Статьи |
| Контакты |
|
|

Обязательна ссылка на источник при использовании данных материалов
|
|||||||||||||||||||||||||||||||||||||||||||||||
Алейников С. М., Вахтин А. А., Тюкачев Н. А. Пространственные гранично-элементные сетки в контактных задачах теории упругости. // Тр. всероссийской конф. Прикладная геометрия, построение расчетных сеток и высокопроизводительные вычисления. - М.: ВЦ РАН, 2004. - Т. 2 - С. 61 - 72. |
|||||||||||||||||||||||||||||||||||||||||||||||
| Назад | |||||||||||||||||||||||||||||||||||||||||||||||
|
ПРОСТРАНСТВЕННЫЕ
ГРАНИЧНО-ЭЛЕМЕНТНЫЕ СЕТКИ В КОНТАКТНЫХ Алейников С.М.*, Вахтин А.А.†, Тюкачев Н.А.†*Воронежский государственный
архитектурно-строительный университет †Воронежский государственный
университет E-mail: alasmbkb@box.vsi.ru, wishmaster_79@mail.ru, nik@cs.vsu.ru АннотацияВ работе описаны алгоритмы, позволяющие генерировать
пространственную гранично-элементную сетку на конструкциях, поверхность которых
предварительно разбивается на фрагменты, имеющих простейшую топологию. Рассматривается
методика построения гранично-элементной сетки путем композиций
дискретизированных поверхностей. Описана процедура корректировки сетки
добавлением и удалением узлов граничных элементов. Предложенные алгоритмы
реализованы в препроцессоре, генерирующем гранично-элементные сетки для решения
пространственных контактных задач теории упругости. ВведениеПрименение метода граничных элементов для
численного моделирования процессов контактного взаимодействия в теории
упругости требует нанесения на контактную поверхность гранично-элементной
сетки, от качества которой во многом зависит получаемое численное решение [1]. Анализ распространенных в настоящее время программных средств (COSMOS,
ЛИРА, FEM_MODELS, SCAD, ANSYS, Z_SOIL, PLAXIS и др.), позволяющих решать
контактные задачи теории упругости, показал, что почти все они используют
методику конечно-элементного моделирования, а применение метода граничных
элементов для решения пространственных контактных задач только начинается. В виду широкого внедрения метода граничных элементов в практику расчета
и проектирования сложных пространственных конструкций авторами разрабатывается
гранично-элементный программный комплекс для решения пространственных
контактных задач теории упругости с достаточно полной автоматизацией подготовки
данных для инженерных расчетов. 1. Гранично-элементное представление
|
|||||||||||||||||||||||||||||||||||||||||||||||
|
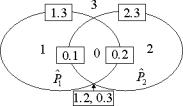
Табл. 1. Нумерация подмножеств |
Рис. 2. Нумерация границ подмножеств |
|
|
0 |
|
|
|
1 |
|
|
|
2 |
|
|
|
3 |
|
|
Без ограничения общности
будем считать, что ![]() . Тогда в общем случае можно рассматривать шестнадцать
множеств, которые могут быть получены в результате логических операций над
двумя множествами
. Тогда в общем случае можно рассматривать шестнадцать
множеств, которые могут быть получены в результате логических операций над
двумя множествами ![]() и
и ![]() . Каждому множеству сопоставляется четырехразрядный двоичный
код, где единица в i-м бите означает, что
элементы i-го подмножества из табл. 1 принадлежат
полученному множеству (табл. 2).
. Каждому множеству сопоставляется четырехразрядный двоичный
код, где единица в i-м бите означает, что
элементы i-го подмножества из табл. 1 принадлежат
полученному множеству (табл. 2).
|
Табл. 2. Двоичная нумерация
множеств, полученных в результате логических операций |
|||
|
0000 |
|
1000 |
|
|
0001 |
|
1001 |
|
|
0010 |
|
1010 |
|
|
0011 |
|
1011 |
|
|
0100 |
|
1100 |
|
|
0101 |
|
1101 |
|
|
0110 |
|
1110 |
|
|
0111 |
|
1111 |
|
Следует заметить, что
вычисление логических выражений сводится к логическим бинарным операциям над
кодами множеств, поэтому для вычислений логических выражений достаточно иметь![]() коды множеств
коды множеств ![]() и
и ![]() .
.
Каждому граничному элементу
геометрических объектов ![]() и
и ![]() , которым соответствуют множества
, которым соответствуют множества ![]() и
и ![]() , сопоставляется индекс, состоящий из номеров подмножеств
(таб. 1), которые они разделяют:
, сопоставляется индекс, состоящий из номеров подмножеств
(таб. 1), которые они разделяют: ![]() где
где ![]() – номер подмножества,
которое охватывает поверхность геометрического объекта,
– номер подмножества,
которое охватывает поверхность геометрического объекта, ![]() – номер внешнего
множества (рис. 2). Аналогично каждой паре различных битов в двоичном
представлении множества сопоставим индексы
– номер внешнего
множества (рис. 2). Аналогично каждой паре различных битов в двоичном
представлении множества сопоставим индексы ![]() где
где ![]() – номер единичного
бита,
– номер единичного
бита, ![]() – номер нулевого
бита. Полученные индексы граничных элементов совпадают с парой номеров
различных битов в двоичном представлении кода операции [2], в случае, когда
– номер нулевого
бита. Полученные индексы граничных элементов совпадают с парой номеров
различных битов в двоичном представлении кода операции [2], в случае, когда ![]() требуется изменить
направление обхода вершин данного граничного элемента (инверсия). Например, в
операции вычитания (
требуется изменить
направление обхода вершин данного граничного элемента (инверсия). Например, в
операции вычитания (![]() ) различны пары битов 1.0, 1.2 и 1.3, что соответствует
граничным элементам с индексами 0.1, 1.2, 1.3, а элементы с индексом 0.1
инвертируются.
) различны пары битов 1.0, 1.2 и 1.3, что соответствует
граничным элементам с индексами 0.1, 1.2, 1.3, а элементы с индексом 0.1
инвертируются.
Данный алгоритм позволяет
без труда вычислять любые операции композиций и выделять граничные элементы,
соответствующие искомому решению и учитывать локальную нумерацию вершин
граничных элементов, что весьма важно при использовании метода граничных
элементов.
3. Корректировка гранично-элементной сетки
Для корректировки гранично-элементных сеток
предложены подходы, основанные на алгоритмах автоматического моделирования многогранников
[2], считая узлы гранично-элементной сетки вершинами, а граничные элементы –
гранями. Корректировка гранично-элементной сетки сводится к добавлению и удалению
граничных элементов и узлов сетки. Сложность поставленной задачи заключается в
том, что требуется автоматически определять локальную нумерацию узлов
добавляемых граничных элементов, чтобы обход вершин грани был против часовой
стрелки при наблюдении с внешней стороны поверхности конструкции (ориентация
граничных элементов).
3.1. Добавление нового узла гранично-элементной сетки
Добавление нового узла заключается в
построении ребер и граней, соединяющих заданную свободную точку с узлами
гранично-элементной сетки. Для однозначного определения ориентации добавляемых
граничных элементов новая вершина соединяется с вершинами, лежащими на одном граничном
элементе.
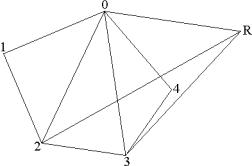
Рис. 3. Корректировка гранично-элементной сетки добавлением узла R
На рис. 3 изображен пример добавления новой
вершины R, которая
соединяется с вершинами 0, 2, 3. Фиксированная грань разбивается на части с целью
выделения и удаления области, образованной вершинами 0, 2, 3. Так как
фиксированная грань ориентирована, то ориентацию характеризуют векторы ![]()
![]() и
и ![]() Это способствует
заданию ориентации новых граней [0, 2, R], [2, 3, R] и [3, 0, R].
Это способствует
заданию ориентации новых граней [0, 2, R], [2, 3, R] и [3, 0, R].
Данный алгоритм дает возможность добавлять не только новые вершины, но и новые граничные элементы, если за свободную точку взять узел гранично-элементной сетки.
3.2. Удаление узла гранично-элементной сетки
Сложность удаления узла гранично-элементной
сетки заключается в том, что если у удаляемой вершины имеется четыре или более
соседних вершин не лежащих в одной плоскости, то это приводит к неоднозначности
в создании новых граней, а значит – к различным вариантам результата удаления.
Поэтому разработано не само удаление, а отсечение части многогранника,
выделенного четырьмя вершинами. Это позволяет сохранить единственность решения
и удалить намеченную вершину за конечное число шагов.
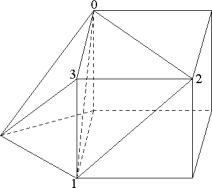
Рис. 4. Корректировка гранично-элементной сетки удалением узла 3 относительно
трех смежных вершин 0, 1, 2
Граничные элементы, на которых лежат два
выделенных и удаляемый узел (далее они называются фиксированными узлами),
разбиваются. Удаляются граничные элементы, образованные тремя фиксированными
узлами. Если фиксированные узлы не лежат на одном граничном элементе, то добавляется
новый граничный элемент с учетом ориентации, которая задается соответствующим
направлением ребер смежных граничных элементов (на рис. 4 это грань [0, 3,
1], ориентация которой задается векторами ![]() и
и ![]() ).
).
На рис. 4 приведен пример удаления узла 3 относительно трех смежных вершин 0, 1, 2: вырезаются, а затем удаляются граничные элементы [1, 2, 3] и [0, 3, 2], с учетом ориентации смежных граничных элементов добавляются грани [0, 3, 1] и [0, 1, 2].
3.3. Дополнительные алгоритмы, применяемые
при корректировке гранично-элементной сетки
Помимо основных алгоритмов добавления и удаления узлов могут потребоваться специальные алгоритмы для корректировки гранично-элементной сетки:
· Изменение пространственного положения узла – изменяются координаты узла, что соответственно влечет за собой изменение пространственного положения граничных элементов, имеющих общим данный узел.
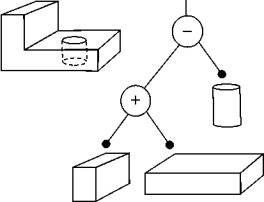
· Интеграция граничных элементов – объединение нескольких граничных элементов, имеющих общие ребра и лежащих в одной плоскости. Объединение основано на построении нового ориентированного граничного элемента, содержащего все ребра объединенных.
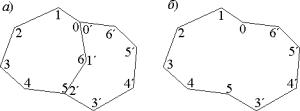
Рис. 5. Интеграция граничных элементов:
а) до интеграции; б) после интеграции
Алгоритм интеграции следующий: проводится обход вершин в первом граничном элементе с включением их в новый, если встретится общий узел, то обход вершин продолжается на следующем граничном элементе до тех пор, пока не вернемся в вершину, с которой был начат обход. Для начала обхода всегда выбирается вершина, не являющаяся общей, так как если начать алгоритм с общей вершины, то можно получить неверное решение. На рис. 5 рассмотрен пример интеграции граней [0, 1, 2, 3, 4, 5, 6,] и [0´, 1´, 2´, 3´, 4´, 5´, 6´].
Во время редактирования, приходится не только объединять граничные элементы, но и вычитать, если их лицевые стороны противоположны. Данный алгоритм предусматривает и этот случай.
· Дискретизация граничных элементов – доразбиение некоторых граничных элементов, полученных в результате построений, для чего используются алгоритмы дискретизации плоских граничных макроэлементов (п. 1.1).
· Проверка гранично-элементной сетки на правильность – на каждом шаге построения требуется проверить отсутствие пересечений и перекрытий граничных элементов, правильность их ориентации, непрерывность поверхности, образованной граничными элементами и другие геометрические свойства, характеризующие корректность действий разработчика. На практике, в зависимости от требований к решаемым контактным задачам, метод проверки гранично-элементной сетки на правильность может содержать геометрические задачи различной сложности.
4. Препроцессор, осуществляющий генерацию гранично-элементой сетки
Разработанные алгоритмы позволяют генерировать
гранично-элементные сетки на поверхностях весьма сложной формы. Они
характеризуются простой логической структурой и небольшими затратами счетного
времени. Существует возможность корректировки, сгущения и перестройки существующих
гранично-элементных сеток в процессе подготовки данных для инженерных расчетов
и проектирования.
На основе построенных алгоритмов разработан препроцессор, позволяющий эффективно генерировать гранично-элементные сетки для решения пространственных контактных задач [1, 3]. Имеется возможность связи препроцессора с существующими программными комплексами на уровне обмена файлов данных, разрабатывая и подключая соответствующие утилиты. Программная реализация, основанная на СОМ-технологии, дает возможность расширения и модификации данного программного продукта путем разработки новых утилит проектирования.
Перечисленные возможности препроцессора, осуществляющего генерацию пространственных гранично-элементных сеток, позволяют без труда адаптировать разработанный программный продукт для различных типов задач, решаемых методом граничных элементов.
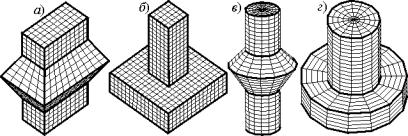
Рис. 6. Гранично-элементная сетка на поверхностях фундаментных конструкций: а)
щелевой с боковыми уширениями; б) столбчатый с одной ступенью; в)
осесимметричный с уширением ствола; г) из цилиндрических составляющих
Для построения гранично-элементной сетки на фундаментных конструкциях, широко распространенных при строительстве промышленных и гражданских объектов [1], используются утилиты генерации гранично-элементной сетки на поверхностях блочного и осесимметричного типов. Некоторые примеры результатов работы данных утилит представлены на рис. 6.
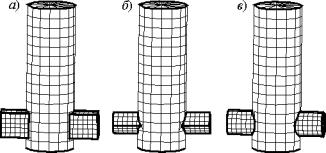
Рис. 7. Дискретизированная поверхность фундаментных конструкций, полученных в
результате пересечений сваи с ригелями различной формы:
а) прямоугольной; б) треугольной призматической; в)
цилиндрической
Утилита композиций позволяет получать дискретизацию поверхностей фундаментных конструкций сложной формы. Например, на рис. 7 предложено конструктивное решение повышения несущей способности свайных цилиндрических опор с использованием ригелей различной формы.
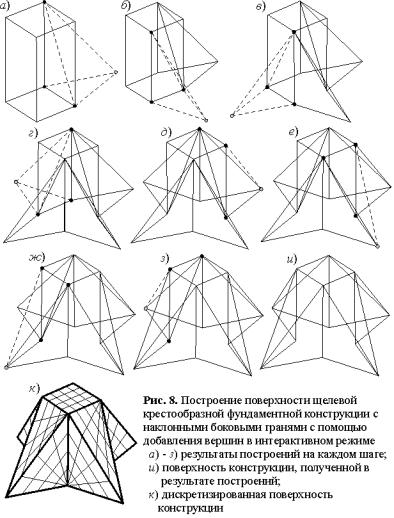
Для возможности построения поверхностей фундаментных конструкций сложной формы в интерактивном режиме разработана утилита с реализованными методами корректировки гранично-элементной сетки. На рис. 8 приведено пошаговое построение поверхности щелевой крестообразной фундаментной конструкции с наклонными боковыми гранями и ее дискретный аналог.
Разработанные утилиты позволяют создавать сложные поверхности фундаментов и генерировать на них гранично-элементные сетки с заданными свойствами.
Список литературы
1.
Алейников С. М. Метод граничных элементов в
контактных задачах для упругих пространственно неоднородных оснований. – М.:
Изд-во «АСВ», 2000. – 754 с.
2.
Тюкачев Н. А., Свиридов Ю. Т. Delphi 5. Создание мультимедийных
приложений. – М.: Нолидж, 2000. – 384 с.
3.
Вахтин А. А.
Программный пакет автоматизированного твердотельного проектирования //
Информатика: проблемы, методология, технологии: Мат. 3-й регион. науч.-мет. конф.
– Воронеж: ВГУ, 2003. – С. 29-32.
Материалы, опубликованные в данном сайте являются авторской интеллектуальной собственностью
и не могут быть использованы ни в каких целях и в никакой форме без письменного разрешения автора