Вахтин А. А., асп., ассистент

Воронежский государственный университет, факультет компьютерных наук, каф. ПиИТ

 

АВТОМАТИЗАЦИЯ ПОСТРОЕНИЯ ГРАНИЧНО-ЭЛЕМЕНТНЫХ СЕТОК ДЛЯ РЕШЕНИЯ СТАТИЧЕСКИХ ЗАДАЧ ТЕОРИИ УПРУГОСТИ

 

Решение статистических задач теории упругости до сих пор остается одной из актуальных задач. Например, известно, что одной из ответственных работ, требующих больших материальных затрат, является строительство фундаментов, свай, штампов и других опорных конструкций, от качества которых зависит не только износостойкость, но и безопасность бытовых и технических сооружений [4].

Для расчета физических характеристик опорных конструкций в настоящее время большую популярность приобретает вычислительный эксперимент, так как натурный и лабораторный эксперимент до сих пор остается сложным, длительным и дорогим, а упрощенные формулы механики грунтов, основанные на аналитических решениях простейших задач, не обеспечивают надежности в процессах проектирования. Вычислительный эксперимент заключается в моделировании напряженно-деформированных состояний грунтовых оснований и фундаментов посредством численного решения уравнений математической физики.

Для решения статистических задач теории упругости существует два основных численных метода: метод конечных элементов (МКЭ) и метод граничных элементов (МГЭ). В МКЭ бесконечная область грунтового основания заменяется конечной, однако трудоемкость решения трехмерных задач до сих пор остается весьма существенной. По сравнению с МКЭ, применение МГЭ упрощает подготовку исходных данных, сокращает затраты счетного времени и памяти ЭВМ, так как свободная поверхность оснований не нуждается в дискретизации на граничные элементы. Важной особенностью МГЭ является то, что подготовка исходных данных практически полностью сводится к детальной дискретизации сложных поверхностей фундаментных конструкций. Благодаря своей наглядности и индифферентности к геометрии МГЭ является в настоящее время наиболее эффективным численным методом для решения статических задач теории упругости [2].

Благодаря развитию математических подходов, аппаратных возможностей вычислительной техники, программных и операционных систем появилась возможность разрабатывать программы с удобным пользовательским интерфейсом, трехмерное моделирование стало визуальным и интерактивным. При этом все вычисления возлагаются на компьютер, а пользователю предоставляются возможности выбора методов решения, задания геометрических и механических параметров, а также возможность возврата к предыдущему шагу на промежуточном этапе. Интенсивное развитие компьютерной индустрии предоставляет расширенные возможности проектирования, но при этом даже современные программные пакеты со временем устаревают и теряют актуальность, что заставляет разработчиков создавать новые программные комплексы.

Во всех существующих программных комплексах, позволяющих решать статические задачи теории упругости (COSMOS, ЛИРА, FEM_MODELS, SCAD, ANSYS, Z_SOIL, PLAXIS и др.), расчет конструкций сводится к следующим основным этапам:

1)      подготовка данных к расчетам (препроцессор);

2)      численное решение пространственных статических задач теории упругости;

3)      эффективная визуализация промежуточных расчетов (для оценки качества решения и корректировки проектных параметров в случае неудовлетворения решения предъявленным требованиям);

4)      оформление окончательных результатов в виде иллюстраций и таблиц.

Из всех перечисленных этапов самым сложным является построение пространственной гранично-элементной сетки на поверхности рассчитываемой конструкции (подготовка данных к расчетам), от качества которой во многом зависит численное решение.

Необходимым условием к разбиению поверхностей опорных конструкций на граничные элементы является отсутствие пересечений и перекрытий, а точки на сложной поверхности должны быть узлами смежных граничных элементов. Локальная нумерация узлов на каждом элементе берется против часовой стрелки при наблюдении со стороны внешней к контактной поверхности нормали (то есть со стороны грунта). В общем случае гранично-элементная сетка состоит из треугольных и четырехугольных граничных элементов [2].

Существующие и разрабатываемые алгоритмы построения гранично-элементной сетки можно разбить на два типа:

1)     алгоритмы генерации гранично-элементной сетки – алгоритмы, которые моделируют с заданными параметрами сетку на поверхностях конструкций с известной топологией (например, осесимметричные или блочные конструкции [1]);

2)     алгоритмы редактирования гранично-элементной сетки – алгоритмы, направленные на редактирование существующей гранично-элементной сетки (например, разбиение, добавление или удаление граничных элементов).

Алгоритмы генерации гранично-элементной сетки основаны на фрагментальной дискретизации, что соответствует предварительному разбиению поверхности рассчитываемой конструкции на граничные макроэлементы [1]. В качестве граничных макроэлементов принимаются поверхностные фрагменты, имеющие простейшую топологию. Как правило, это плоские треугольники и четырехугольники, части цилиндрических, конических и сферических поверхностей. В отдельных случаях используются граничные макроэлементы, уравнения поверхности которых могут быть заданы детерминировано.

Граничные макроэлементы разбиваются на отдельные граничные элементы с автоматической генерацией координат и узлов. Разбиение производится регулярно и не обязательно равномерно. Степень неравномерности разбиения в отдельном граничном макроэлементе по различным направлениям задается параметрически и, по возможности, учитывает предполагаемый характер изменения контактных напряжений. Важным аспектом фрагментальной дискретизации является согласование по числу граничных элементов на линиях сопряжения сложных граничных макроэлементов. Это необходимо для улучшения численного решения и удобства при обработке и интерпретации полученных результатов.

Разбиение четырехугольных граничных макроэлементов на отдельные элементы производится на основе техники изопараметрических элементов [1]. Описание геометрии в плоскости четырехугольного граничного макроэлемента получается с использованием интерполяционных формул. Если на стандартном квадрате берется равномерная или сгущающаяся к границе сетка элементов, то линейное изопараметрическое преобразование переведет их в глобальные граничные элементы без нарушения межэлементной непрерывности и с требуемой регулярной нумерацией узлов и вершин.

Интерполяционные формулы для дискретизации треугольных граничных макроэлементов могут быть получены из интерполяционных формул дискретизации четырехугольных с учетом того, что две смежные вершины сливаются в одну. В результате формируется алгоритм дискретизации треугольных граничных макроэлементов, который весьма просто позволяет добиваться необходимой степени густоты гранично-элементной сетки. При разбиении треугольных макроэлементов в качестве вершины сгущения не рекомендуется брать острые углы, так как при дискретизации может появиться большое количество граничных элементов с общей вершиной, площадь которых близка к нулю.

Дискретизация произвольного плоского макроэлемента сводится к разбиению его на четырехугольные и треугольные фрагменты, которые, в свою очередь, разбиваются на отдельные граничные элементы по предложенным выше алгоритмам.

Разбиение осесимметричных граничных макроэлементов осуществляется также с помощью плоских треугольных и четырехугольных граничных элементов путем меридиональных и горизонтальных сечений фрагментов канонической формы (цилиндрических, конических, сферических). Полная дискретизация поверхности фундаментной конструкции в виде тела вращения получается в результате объединения граничных макроэлементов простейших форм. При достаточно малых размерах граничных элементов, исходя из физических представлений естественно ожидать, что контактное взаимодействие и деформирование конструкции (после аппроксимации поверхности ансамблем плоских граничных элементов) под действием внешней нагрузки будет немногим отличаться от поведения реального объекта, и что приближенное решение контактной задачи будет сходиться к точному. Практические расчеты показывают, что сходимость действительно имеет место, причем достаточно хорошая [1].

Далее рассмотрены алгоритмы редактирования существующей гранично-элементной сетки.

Конструкции, имеющие сложную топологию поверхности, можно представить в виде композиций простых геометрических объектов, разбиение поверхностей которых тривиальна или уже известна.

Без ограничения общности будем считать, что поверхности двух геометрических объектов  и , охватывающих пространственные множества  и  соответственно, ограничивают четыре непересекающихся подмножества (рис. 1), нумерация которых задается согласно табл. 1.

 

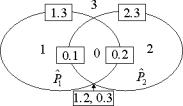
Тогда в общем случае можно рассматривать шестнадцать множеств, которые могут быть получены в результате логических операций над двумя множествами  и . Каждому множеству сопоставляется четырехразрядный двоичный код, где единица
в i-м бите означает, что элементы i-го подмножества из табл. 1 принадлежат полученному множеству (табл. 2).

 

 

Из табл. 2 очевидно, что вычисления логических выражений сводятся к логическим бинарным операциям над кодами множеств  и

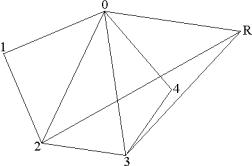
Каждому граничному элементу геометрических объектов  и , которым соответствуют множества  и , сопоставляется индекс, состоящий из номеров подмножеств (таб. 1), которые они разделяют:  где  – номер подмножества, которое охватывает поверхность геометрического объекта,  – номер внешнего множества (рис. 1). Аналогично каждой паре различных битов в двоичном представлении множества сопоставим индексы  где  – номер единичного бита,  – номер нулевого бита. В итоге полученные индексы граничных элементов совпадают с парой номеров различных битов в двоичном представлении кода операции. В случае, когда  требуется изменить направление обхода вершин данного граничного элемента (инверсия). Например, в операции вычитания ( ) различны пары битов 1.0, 1.2 и 1.3, что соответствует граничным элементам с индексами 0.1, 1.2, 1.3, при этом элементы с индексом 0.1 инвертируются.

Данный алгоритм позволяет без труда вычислять любые операции композиций и выделять граничные элементы, соответствующие искомому решению и учитывать локальную нумерацию вершин граничных элементов, что весьма важно при использовании метода граничных элементов.

Для корректировки гранично-элементных сеток предложены подходы, основанные на добавлении и удалении граничных элементов и узлов сетки. Сложность поставленной задачи заключается в том, что требуется автоматически определять локальную нумерацию узлов добавляемых граничных элементов, чтобы обход вершин грани был против часовой стрелки при наблюдении с внешней стороны поверхности конструкции (ориентация граничных элементов).

Добавление нового узла заключается в построении ребер и граней, соединяющих заданную свободную точку с узлами гранично-элементной сетки. Для однозначного определения ориентации добавляемых граничных элементов новая вершина соединяется с вершинами, лежащими на одном граничном элементе.

На рис. 2 изображен пример добавления новой вершины R, которая соединяется с вершинами 0, 2, 3. Фиксированная грань разбивается на части с целью выделения и удаления области, образованной вершинами 0, 2, 3. Так как фиксированная грань ориентирована, то ориентацию характеризуют векторы    и  Это способствует заданию ориентации новых граней [0, 2, R], [2, 3, R] и [3, 0, R].

Данный алгоритм дает возможность добавлять не только новые вершины, но и новые граничные элементы, если за свободную точку взять узел гранично-элементной сетки.

Сложность удаления узла гранично-элементной сетки заключается в том, что если у удаляемой вершины имеется четыре или более соседних вершин не лежащих в одной плоскости, то это приводит к неоднозначности в создании новых граней, а значит – к различным вариантам результата удаления. Поэтому разработано не само удаление, а отсечение части многогранника, выделенного четырьмя вершинами. Это позволяет сохранить единственность решения и удалить намеченную вершину за конечное число шагов.

Граничные элементы, на которых лежат два выделенных и удаляемый узел (далее они называются фиксированными узлами), разбиваются. Удаляются граничные элементы, образованные тремя фиксированными узлами. 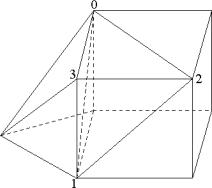Если фиксированные узлы не лежат на одном граничном элементе, то добавляется новый граничный элемент с учетом ориентации, которая задается соответствующим направлением ребер смежных граничных элементов (на рис. 4 это грань [0, 3, 1], ориентация которой задается векторами  и ).

На рис. 3 приведен пример удаления узла 3 относительно трех смежных вершин 0, 1, 2: вырезаются, а затем удаляются граничные элементы [1, 2, 3] и [0, 3, 2], с учетом ориентации смежных граничных элементов добавляются грани [0, 3, 1] и [0, 1, 2].

 

Рис. 2. Корректировка гранично-элементной сетки добавлением узла R

Рис. 3. Корректировка гранично-элементной сетки удалением узла 3 относительно трех смежных вершин 0, 1, 2

 

Помимо основных алгоритмов добавления и удаления узлов могут потребоваться специальные алгоритмы для корректировки гранично-элементной сетки, как, например, изменение пространственного положения узла, объединение и дискретизация граничных элементов, и т. п. Данные алгоритмы в статье рассматриваться не будут в виду их простоты реализации.

Разработанные алгоритмы позволяют генерировать гранично-элементные сетки на поверхностях весьма сложной формы. Они характеризуются простой логической структурой и небольшими затратами счетного времени. Существует возможность корректировки, сгущения и перестройки существующих гранично-элементных сеток в процессе подготовки данных для инженерных расчетов и проектирования.

На основе предложенных алгоритмов реализованы утилиты для препроцессора гранично-элементного программного комплекса [3]. Программная реализация препроцессора, основанная на СОМ-технологии, дает возможность расширения и модификации данного программного продукта путем разработки новых утилит проектирования. Также имеется возможность связи препроцессора с существующими программными комплексами на уровне обмена файлов данных, разрабатывая и подключая соответствующие утилиты.

Перечисленные возможности препроцессора, осуществляющего генерацию пространственных гранично-элементных сеток, позволяют без труда адаптировать разработанный программный продукт для различных типов задач, решаемых методом граничных элементов.

 

Список использованных источников:

1. Алейников С. М. Метод граничных элементов в контактных задачах для упругих пространственно неоднородных оснований. – М.: Изд-во «АСВ», 2000. – 754 с.
2. Бреббия К., Теллес Ж., Вроубел Л. Методы граничных элементов: Пер. с англ. – М.: Мир, 1987. – 524 с.
3. Вахтин А. А. Препроцессор гранично-элементного программного комплекса для решения задач геотехники // Системы управления и информационные технологии. – 2003/ – № 1-2. С. 68 – 72.
4. Гибшман Е. Е., Назаренко Б. П. Мосты и сооружения на дорогах. – Ч. I. – М.: Транспорт, 1972. – 408 с.