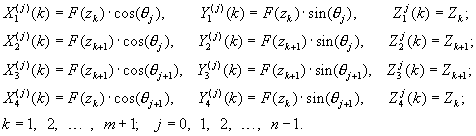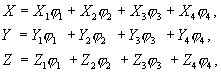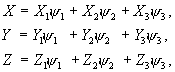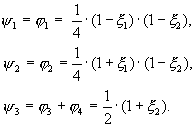ГЕНЕРАЦИЯ ГРАНИЧНО-ЭЛЕМЕНТНЫХ СЕТОК ДЛЯ РАСЧЕТА ОСНОВАНИЙ И ФУНДАМЕНТОВ МОСТОВЫХ ОПОР В ПРОСТРАНСТВЕННОЙ ПОСТАНОВКЕ

 

Алейников С. М., Вахтин А. А.

 

Аннотация: Рассматриваются методы дискретизации поверхностей фундаментных конструкций сложной формы, применяемых в дорожно-транспортном строительстве. Описаны структура и функциональные возможности программного модуля URAN, предназначенного для автоматизированной подготовки данных при численном решении пространственных контактных задач в фундаментостроении методом граничных элементов.

 

THE GENERATION OF BOUNDARY-ELEMENT GRIDS FOR CALCULATION OF THE BASIS AND FOUNDATIONS OF BRIDGE BEARINGS BY SPACE SETTING

 

Aleynikov S. M., Vahtin A. A.

 

Abstract: the methods of digitization of surfaces of foundation constructions of complex form used in road and transport building are considered. The frame and functional capabilities of a program module URAN, intended for computer-based training of the data at solution of the space contact tasks of foundation building by boundary-element method are described

 

Введение. В дорожно-транспортном строительстве одной из ответственных работ, требующих больших материальных затрат, является проектирование и расчет оснований и фундаментов мостовых опор. Мост как ответственное сооружение должен удовлетворять ряду требований производственного, эксплуатационного, расчетно-конструктивного, экономического и архитектурного характера [4], что требует тщательных инженерно-изыскательских работ и решения ряда сложных задач геотехники и строительной механики.

В последнее время в геотехническом строительстве все большую популярность приобретает вычислительный эксперимент, так как натурный и лабораторный эксперимент до сих пор остается сложным, длительным и дорогим, а упрощенные формулы механики грунтов, основанные на аналитических решениях простейших задач, не обеспечивают надежности в процессах проектирования. Вычислительный эксперимент заключается в моделировании напряженно-деформированных состояний грунтовых оснований и фундаментов посредством численного решения уравнений математической физики. Используется два основных численных метода в геотехнических расчетах: метод конечных элементов (МКЭ) и метод граничных элементов (МГЭ). В МКЭ бесконечная область грунтового основания заменяется конечной, однако трудоемкость решения трехмерных задач до сих пор остается весьма существенной. По сравнению с МКЭ, применение МГЭ упрощает подготовку исходных данных, сокращает затраты счетного времени и памяти ЭВМ в виду то, что свободная поверхность оснований не нуждается в дискретизации на граничные элементы. Важной особенностью МГЭ является то, что подготовка исходных данных практически полностью сводится к детальной дискретизации сложных поверхностей фундаментных конструкций. Благодаря своей наглядности и индифферентности к геометрии МГЭ является в настоящее время наиболее эффективным численным методом для решения пространственных контактных задач в геотехнике [1].

Интенсивное развитие компьютерной индустрии дает расширенные возможности проектирования, но при этом даже универсальные программные пакеты со временем устаревают и теряют актуальность. Поэтому разработка программных комплексов автоматизированного проектирования фундаментов мостовых опор остается все еще актуальной, что заставляет разработчиков создавать новые программные комплексы. Современные математические подходы, аппаратные возможности вычислительной техники, программных и операционных систем позволяют разрабатывать универсальные программные пакеты с удобным пользовательским интерфейсом. Появилась возможность сделать трехмерное моделирование визуальным и интерактивным. При этом все вычисления возлагаются на компьютер, а пользователю предоставляются возможности выбора методов решения, задания геометрических и механических параметров, а также возврат на промежуточном этапе к предыдущему шагу.

В связи с широким внедрением МГЭ в практику проектирования и расчетов фундаментных конструкций авторами разработан и совершенствуется гранично-элементный программный комплекс для расчета геотехнического строительства с практически полной автоматизацией инженерных расчетов.

Анализ распространенных в настоящее время программных средств, позволяющих решать контактные задачи геотехники и фундаментостроения (COSMOS, ЛИРА, FEM_MODELS, SCAD, ANSYS, Z_SOIL, PLAXIS и др.) показал, что все они используют методику конечно-элементного моделирования, а применение МГЭ для решения задач геотехнического строительства только начинается. Во всех существующих программных комплексах расчет фундамента сводится к следующим основным этапам:

1)      подготовка данных к расчетам (препроцессор);

2)      численное решение пространственных контактных задач взаимодействия фундаментных конструкций с грунтом;

3)      эффективная визуализация промежуточных расчетов (для оценки качества решения и корректировки проектных параметров в случае неудовлетворения решения предъявленным требованиям);

4)     оформление окончательных результатов в виде иллюстраций и таблиц.

Далее рассмотрены математические методы гранично-элементного разбиения поверхностей, реализованных в утилитах программного модуля URAN, предназначенного для автоматизированной подготовки данных при гранично-элементном решении пространственных контактных задач в фундаментостроении.

1. Гранично-элементное представление поверхностей фундаментных конструкций сложной формы. Разбиение в общем случае предполагается смешанным, то есть с одновременным присутствием треугольных и четырехугольных граничных элементов. Необходимым условием к разбиению поверхностей фундаментных конструкций на граничные элементы является отсутствие пересечений и перекрытий, а точки на сложной поверхности должны быть узлами смежных граничных элементов. Локальная нумерация узлов на каждом элементе берется против часовой стрелки при наблюдении со стороны внешней к контактной поверхности нормали (то есть со стороны грунта).

Для всех типов поверхностей принята фрагментальная дискретизация, что соответствует предварительному разбиению поверхности фундаментной конструкции на граничные макроэлементы [1]. В качестве граничных макроэлементов принимаются поверхностные фрагменты, имеющие простейшую топологию. Как правило, это плоские треугольники и четырехугольники, части цилиндрических, конических и сферических поверхностей. В отдельных случаях используются граничные макроэлементы, уравнения поверхности которых могут быть заданы детерминировано.

Граничные макроэлементы разбиваются на отдельные граничные элементы с автоматической генерацией координат и узлов. Разбиение производится регулярно и не обязательно равномерно. Степень неравномерности разбиения в отдельном граничном макроэлементе по различным направлениям задается параметрически и, по возможности, учитывает предполагаемый характер изменения контактных напряжений. Важным аспектом фрагментальной дискретизации является согласование по числу граничных элементов на линиях сопряжения сложных граничных макроэлементов. Это необходимо для улучшения численного решения и удобства при обработке и интерпретации полученных результатов.

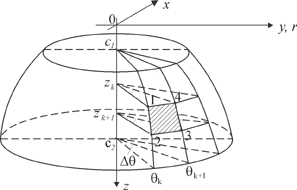
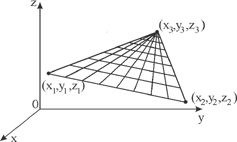
На практике в основном используются два вида фундаментных конструкций: осесимметричные фундаменты и фундаменты блочного типа, методы дискретизации которых будет рассмотрена далее.

1.1. Осесимметричные фундаментные конструкции. Осесимметричная поверхность получается в результате вращения некоторой кривой вокруг оси симметрии. Полагаем, что осью симметрии является ось OZ (рис. 1). Тогда уравнение поверхности в цилиндрической системе координат имеет вид

 

   .

 

Для нанесения сетки граничных элементов на поверхность вращения отрезок  делим на m не обязательно равных частей точками (рис. 1)

 

   

 

где  – функция, отображающая отрезок  в себя и подбираемая в зависимости от вида F(z) для сгущения точек деления у концов отрезка; a – параметр сгущения.

 

Рис. 1. Дискретизация поверхности вращения на граничные элементы

 

Интервал  изменения угловой координаты q разбиваем на n равных частей плоскостями  (j=0, 1, …, n-1) с шагом . Рассматривая каждые два последовательных меридиональных сечения    формируем плоские граничные элементы путем вычисления координат вершин по формулам

 

 

Следует заметить, что в случае, когда F(z)=0 (концевая точка фундаментной конструкции), вторая и третья вершины у граничных элементов сливаются в одну и четырехугольные элементы вырождаются в треугольные. Общее количество плоских граничных элементов на рассмотренном теле вращения будет равно и растет с увеличением числа разбиений как по глубине (m), так и по угловой координате (n).

В соответствии с принятой терминологией аппроксимируемый фрагмент поверхности вращения с использованием плоских четырехугольных и треугольных граничных элементов будет представлять собой граничный макроэлемент на теле вращения. Разработаны процедуры автоматической дискретизации граничных макроэлементов для наиболее часто встречающихся фрагментов поверхностей вращения

 

                                   цилиндрической:

                                   конической:

                                   сферической:

 

где R – радиус цилиндра или сферы;  – радиусы верхнего и нижнего оснований усеченного конуса соответственно;  – аппликата центра сферы.

Для случаев, когда поверхность тела вращения задается с помощью уравнения вида

 

применяется еще один, достаточно эффективный способ дискретизации макроэлементов, более удобный, чем рассмотренный выше. Используется тот факт, что любой фрагмент поверхности вращения, заключенный между плоскостями  и , всегда имеет своей проекцией в плоскости XOY круг или кольцо. Тогда, имея дискретизацию этих плоских канонических областей и применяя указанную выше функциональную зависимость, легко осуществляется аппроксимация граничных макроэлементов на телах вращения плоскими граничными элементами треугольного или четырехугольного типов с непосредственным выполнением требований межэлементной непрерывности. В разработанных процедурах для рассмотренного способа разбиения граничных макроэлементов на

 

                                   плоскости:

                                   конической поверхности:

                                   сферической поверхности:

 

использовались регулярные равномерные и неравномерные сетки на круге и кольце, позволяющие получать пространственную дискретизацию нужного качества.

Полная дискретизация поверхности фундаментной конструкции в виде тела вращения получается в результате объединения граничных макроэлементов рассмотренных простейших форм. Когда общее число плоских граничных элементов достаточно велико, а размеры их достаточно малы, то исходя из физических представлений, естественно ожидать, что контактное взаимодействие с грунтом такой фундаментной конструкции (после аппроксимации поверхности ансамблем плоских граничных элементов) под действием внешней нагрузки будет немного отличаться от поведения реального фундамента и что приближенное решение контактной задачи будет сходиться к точному при увеличении числа плоских граничных элементов и уменьшении их размеров. Практические расчеты показывают, что имеет место достаточно хорошая сходимость [1].

1.2. Блочные фундаментные конструкции. Фундаментные конструкции блочного типа определяются заданием глобальных координат узловых точек треугольных или четырехугольных граничных макроэлементов

 

 

Разбиение граничных макроэлементов на отдельные элементы производится на основе техники изопараметрических элементов [1]. Описание геометрии в плоскости четырехугольного граничного макроэлемента получается с использованием интерполяционных формул:

 

 

где  – простейшие линейные функции, имеющие вид:

 

 

Безразмерные переменные  отождествляются с локальными координатами в плоскости стандартного квадрата , . Если на стандартном квадрате берется равномерная (рис. 2, а) или сгущающаяся к границе (рис. 2, б) сетка элементов, то линейное изопараметрическое преобразование переведет их в глобальные граничные элементы без нарушения межэлементной непрерывности и с требуемой регулярной нумерацией узлов и вершин.

 

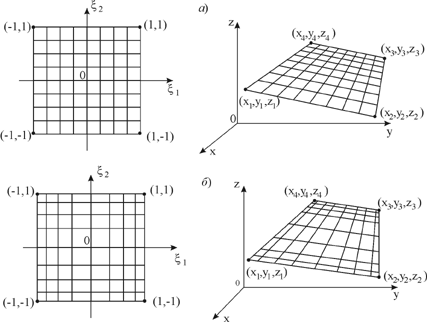
Рис. 2. Локальные координаты для четырехугольного граничного макроэлемента: а) равномерная сетка; б) неравномерная сетка

 

Интерполяционные формулы дискретизации треугольных плоских граней (треугольных граничных макроэлементов) следуют из интерполяционных формул дискретизации четырехугольных граничных макроэлементов, с учетом, что две смежные вершины  и  сливаются в одну:

 

где

 

В результате получаем алгоритм дискретизации треугольных граничных макроэлементов, который весьма просто позволяет добиваться необходимой степени густоты треугольной гранично-элементной сетки (рис. 3). При необходимости полученную гранично-элементную сетку без труда можно сгустить возле выделенной вершины граничного макроэлемента, используя, например, квазиравномерные сетки.

 

Рис. 3. Дискретизация треугольного граничного макроэлемента

2. Структура программного модуля URAN. С учетом описанного выше геометрического подхода к генерации пространственной гранично-элементной сетки разработан программный модуль URAN, обеспечивающий автоматизированную подготовку данных (препроцессор) для решения трехмерных контактных задач, возникающих в фундаментостроении и геотехническом строительстве. Задача препроцессора заключается в построении трехмерной модели фундамента мостовой опоры и генерировать на его поверхности сетку граничных элементов с заданным правилом обхода их узлов.

Программный модуль URAN состоит из основного приложения и динамически подключаемых утилит проектирования. Доступ к подключенным утилитам осуществляется с помощью меню программы, которое создается при запуске приложения. При выборе какой-либо утилиты появляется диалоговое окно ввода параметров и настраиваются соответствующие функциональные возможности работы с мышью. Помимо динамически подключаемых утилит в программу включены стандартные аффинные преобразования: инверсия координат, отражение, поворот, растяжение и перенос.

При разработке программного модуля URAN были учтены следующие требования:

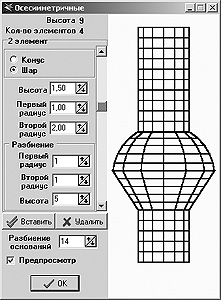
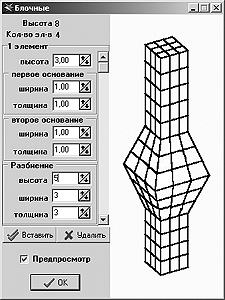
1)     работа с программным модулем должна быть как можно более простой и унифицированной;

2)     затраты времени на подготовку данных и системные требования к ЭВМ должны быть минимизированы;

3)     учтена возможность сопряжения программного модуля с другими общеизвестными пакетами графических или расчетных программ;

4)     должна иметься возможность модификации программного модуля при расширении диапазона задач проектирования.

Для выполнения первого требования в программе URAN разработан стандартный интерфейс, предоставляющий пользователю управлять проектированием и отображать результаты геометрических построений как в трех проекциях (XY, ZY, ZX), так и перспективе (XYZ). Окна проекций используются для возможности проектирования мышью. Например, в утилите <Редактор многогранников> [2] можно менять координаты вершины геометрического объекта с максимальной точностью. Используя пункты меню, окна проекций можно свернуть, спрятать, выстроить каскадом или упорядочить. В процессе геометрических построений можно отменить одно или несколько действий.

Чтобы затраты времени на подготовку данных и системные требования ЭВМ были минимизированы (второе требование, поставленное при разработке программного средства), моделируемый геометрический объект представлен в виде динамической структуры [3], ссылка на которую передается между утилитами и приложением.

Выполнение третьего требования предложено реализовать на уровне файлов данных, сохраняемых на диске в формате, доступном другим приложениям. С этой целью сохранение данных в приложении осуществляется с помощью динамически подключаемых утилит. Данные утилиты разработаны с соблюдением установленных требований независимо от приложения и подключаются как на стадии инсталляции программы, так и к уже установленному пакету [3].

Для возможности модификации и расширения приложения URAN (четвертое требование) программный модуль состоит из нескольких взаимосвязанных блоков: основное приложение, встроенные COM-серверы твердотельного моделирования, встроенные COM-серверы работы с файлами и библиотека типов, которая служит связующим звеном между приложением и COM-сервером [3]. Таким образом, в самой программе осуществляется связь и управление процессом геометрического построения, а сами инструменты находятся во встроенных COM-серверах, называемых «утилитами проектирования». Программный модуль URAN может изменяться и расширяться как на стадии инсталляции, так и при последующих обновлениях. При подключении нового COM-сервера текущие настройки программного пакета сохраняются в системном реестре WINDOWS.

2.1. Утилита генерации гранично-элементной сетки на поверхности осессимметричных фундаментов. Разработанная утилита основана на том, что осесимметричные фундаментные конструкции, применяемые в мостостроении, можно разбить на элементы, боковая поверхность которых имеет цилиндрическую, коническую или сферическую форму, а в основаниях – круговой макроэлемент (рис. 4).

 

Рис. 4. Диалоговое окно утилиты генерации гранично-элементной сетки на поверхности осесимметричных фундаментных конструкций

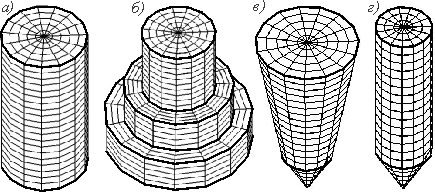
В дорожно-транспортном строительстве весьма широко используются жесткие фундаменты из цилиндрических составляющих (рис. 5, а, б): короткие одиночные буронабивные и буро-опускные сваи, сваи-оболочки небольшой длины, опускные колодцы и колодцы-оболочки.

Не менее эффективны короткие буронабивные сваи из конических составляющих: конические (рис. 5, в) и с коническим заострением (рис. 5, г). Форма боковой поверхности приводит к явно выраженному увеличению несущей способности конических свай за счет формирования зоны уплотнения околосвайного пространства.

 

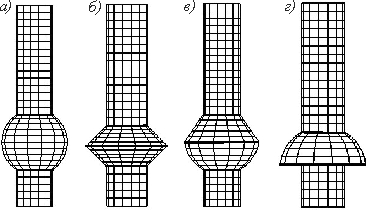
Рис. 5. Примеры разбиения поверхностей осесимметричных фундаментов: а) Цилиндрический; б) телескопический; в) биконический; г)  с коническим острием

 

Значительного эффекта по повышению несущей способности коротких цилиндрических фундаментов удается достигнуть за счет уширения их части ствола (пяты, оголовка или промежутка между ними). На рис. 6, д-з показаны дискретизированные с помощью плоских граничных элементов поверхности цилиндрических фундаментов с различными уширениями. В соответствии с технологией разбуривания грунта форма поверхности уширений определяется сочленением конических, цилиндрических и сферических фрагментов.

 

Рис. 6. Фундаменты с уширением ствола: а) сферическим; б) коническим;
г) сферо-коническим; д) полусферическим

 

Как видно из рис. 6, использование в нужной последовательности круговых, кольцевых, цилиндрических, конических и сферических граничных макроэлементов обеспечивает в автоматическом режиме согласованную дискретизацию поверхностей фундаментных конструкций с различными типами уширений.

2.2. Утилита генерации гранично-элементной сетки на поверхности блочных фундаментов. Фундаментные конструкции, используемые в мостостроении, представляются в виде набора блоков, симметричных относительно некоторой плоскости. Верхним и нижним основанием каждого блока является прямоугольник, ребро или вершина (фундаменты с заострением), боковая поверхность состоит из четырех угольников и, в случае, если в основании ребро или вершина, треугольников. Данные свойства были использованы в утилите твердотельного моделирования (рис. 7).

 

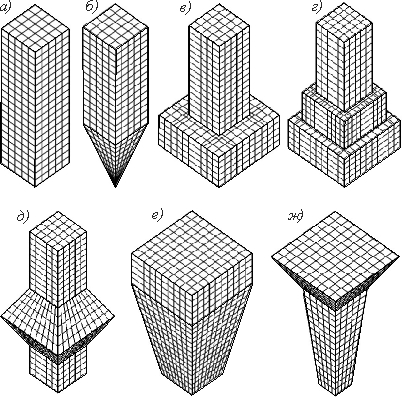
Рис. 7. Диалоговое окно утилиты генерации гранично-элементной сетки на поверхности блочной фундаментной конструкции

На рис. 8 показаны дискретизированные поверхности блочных фундаментов при помощи равномерных сеток из четырехугольных и треугольных (для фундаментов с заострением) граничных микроэлементов. Прямоугольные призматические монолитные бетонные фундаменты с относительным заглублением  (рис. 8, а) широко применяются под мостовые опоры типа опускных колодцев и др. Распространены прямоугольные призматические фундаменты с конструктивными дополнениями: забивные сваи с пирамидальным острием (рис. 8, б), одноступенчатые и многоступенчатые столбчатые фундаменты (рис. 8, в, г), щелевые фундаменты с боковыми уширениями в виде продольных ребер различной конфигурации поперечного сечения (рис. 8, д). В дорожно-транспортном фундаментостроении взамен обычных призматических свай с большой эффективностью по несущей способности при равном объеме используются фундаменты из коротких пирамидальных свай. На рис. 8, е и ж показаны дискретизированные контактные поверхности с грунтом для пирамидальных фундаментов большинства известных форм, хорошо работающие на горизонтальные и моментные нагрузки [4].

Рис. 8. Дискретизированные поверхности блочных фундаментов: а) призматический; б) с пирамидальным заострением; в) и г) ступенчатые;
д) призматичный с уширением; е) и ж) пирамидальные

 

Заключение. Разработанные алгоритмы гранично-элементной дискретизации поверхностей фундаментных конструкций, применяемых в дорожно-транспортном строительстве, характеризуются простой логической структурой и небольшим временем работы ЭВМ. Возможность генерации сгущающихся сеток эффективно для оценки точности численного решения. Предложенное конструирование поверхностных аппроксимаций позволяет многократно автоматически перестраивать сетки, адаптируя их к искомому решению с помощью локальных сгущений.

Реализованные в программном модуле URAN утилиты автоматизированного моделирования, основанные на предложенных в данной работе алгоритмах, позволяют генерировать гранично-элементную сетку на фундаментных конструкциях любой сложности. Подключенные к программному модулю файловые утилиты предоставляют возможность сохранять сгенерированные сетки в файловом формате, доступном другим стандартным пакетам автоматизированного проектирования. В результате программный модуль URAN можно использовать как эффективный предпроцессор для решения контактных задач оснований и фундаментов мостовых опор в пространственной постановке.

 

Библиографический список

 

1.      Алейников С. М. Метод граничных элементов в контактных задачах для упругих пространственно неоднородных оснований. – М.: Изд-во «АСВ», 2000. – 754 с.

2.      Вахтин А. А. Алгоритмы автоматического моделирования многогранников // Математическое обеспечение ЭВМ: Межвуз. сб. научн. тр. – Воронеж: ВГУ, 2002. – Вып. 4. – С. 27-31.

3.      Вахтин А. А. Программный пакет автоматизированного твердотельного проектирования // Информатика: проблемы, методология, технологии: Мат. 3-й регион. науч.-мет. конф. – Воронеж: ВГУ, 2003. – С. 29-32.

4.      Гибшман Е. Е., Назаренко Б. П. Мосты и сооружения на дорогах. – Ч. I. – М.: Транспорт, 1972. – 408 с.