| На главную |
| Структура программы |
| Презентация |
| Статьи |
| Контакты |
|
|

Обязательна ссылка на источник при использовании данных материалов
|
Алейников С. М., Вахтин А. А., Тюкачев Н. А. Система автоматизации построения пространственных сеток для решений контактных задач методом граничных элементов на основе технологии COM. // Вестник ф-та прикладной математики, информатики и механики. - 2005. - № 5 - С. 10 - 18. |
| Назад |
|
УДК: 681.3.07, 519.642 :
593.3 : 624.044 : 624.15 Алейников С. М., Вахтин А. А., Тюкачев Н. А. СИСТЕМА
АВТОМАТИЗИРОВАННОГО ПОСТРОЕНИЯ ПРОСТРАНСТВЕННЫХ СЕТОК ДЛЯ РЕШЕНИЙ КОНТАКТНЫХ
ЗАДАЧ МЕТОДОМ ГРАНИЧНЫХ ЭЛЕМЕНТОВ НА ОСНОВЕ ТЕХНОЛОГИИ СОМ Воронежский
государственный архитектурно-строительный университет Воронежский государственный университет e-mail: alasmbkb@box.vsi.ru, vahtin@vmail.ru, nik@cs.vsu.ru Аннотация. При решении контактных
задач методом граничных элементов самым сложным является построение
пространственной сетки на поверхности конструкции (подготовка данных к
расчетам). Ввиду актуальности данной задачи авторы разработали САПр для
генерации гранично-элементных сеток с возможностью расширения диапазона задач и
методов решений. Annotation. It is very difficult to
construct space grid on surface of construction (data is preparation for
computing) during solution contact problem by boundary elements method. The
authors are developed SAP for generation boundary elements grids which may is
amplify range of solution problems and other methods of solution. Введение. Применение метода граничных
элементов для численного моделирования контактных процессов требует нанесения
на контактную поверхность гранично-элементной сетки, от качества которой во
многом зависит получаемое решение [1]. В виду
актуальности задачи геометрического построения пространственных сеток на
поверхностях конструкций сложных форм, авторами разработана система автоматизированного
построения пространственных гранично-элементных сеток (САПр гранично-элементных
сеток), обеспечивающая автоматизированную подготовку данных (препроцессор) для
решения трехмерных контактных задач. Особенность поставленной задачи заключается
в том, что требуется генерировать на поверхности рассчитываемой конструкции пространственную
гранично-элементную сетку с заданным правилом обхода узлов. Благодаря
развитию математических подходов, аппаратных возможностей вычислительной
техники, программных и операционных систем появилась возможность разрабатывать
программы с удобным пользовательским интерфейсом, трехмерное моделирование стало
визуальным и интерактивным. При этом все вычисления возлагаются на компьютер, а
пользователю предоставляются возможности выбора методов решения, задания геометрических
и механических параметров, а также возможность возврата к предыдущему шагу на
промежуточном этапе. Интенсивное развитие компьютерной индустрии предоставляет
расширенные возможности проектирования, но при этом даже современные
программные пакеты со временем устаревают и теряют актуальность, что заставляет
разработчиков создавать новые программные комплексы. На основе
анализа существующих программных комплексов (COSMOS, ЛИРА, FEM_MODELS, SCAD, ANSYS, Z_SOIL, PLAXIS и
др.) и стандартных требований к программам, при разработке САПр
гранично-элементных сеток были учтены следующие условия: 1) должна иметься возможность
модификации программного модуля при расширении диапазона задач проектирования; 2) учтена возможность
сопряжения программного модуля с другими общеизвестными пакетами графических
или расчетных программ. 3) работа с программным модулем
должна быть как можно более простой и унифицированной; 4) затраты времени на
подготовку данных и системные требования к ЭВМ должны быть минимизированы; Структура
системы автоматизированного построения пространственных гранично-элементных
сеток.
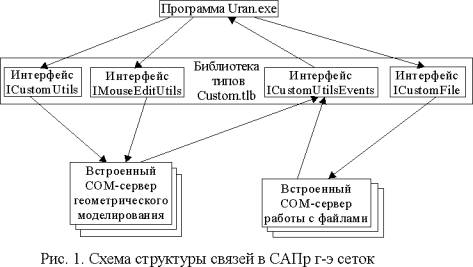
Программно САПр гранично-элементных сеток состоит из нескольких взаимосвязанных
блоков: основное приложение (Uran.exe), встроенные COM-серверы
[5] твердотельного моделирования (утилиты проектирования), встроенные COM-серверы
работы с файлами (файловые утилиты) и библиотека типов (Custom.tlb),
которая служит связующим звеном между приложением и утилитами (рис. 1).
Утилиты можно подключать к программе как на стадии инсталляции, так и при
последующих обновлениях, что обеспечивает гибкие возможности модификации при
расширении диапазона задач проектирования. Настройки САПр гранично-элементных
сеток хранятся в системном реестре WINDOWS и загружаются при запуске
программы.
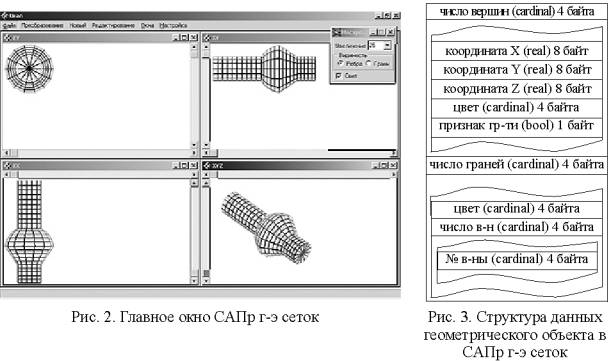
В основном
приложении (рис. 2) осуществляется доступ к утилитам проектирования и
отображение результатов геометрических построений в трех проекциях (XY, ZY, ZX), и
перспективе (XYZ). Окна проекций используются как для визуального
отображения проекций моделируемой конструкции, так и для возможности проектирования
мышью, например, можно менять координаты вершины геометрического объекта с максимальной
точностью, поворачивать фигуру относительно осей координат.
Чтобы затраты времени на подготовку данных и
системные требования ЭВМ были минимизированы, моделируемый геометрический
объект представляет собой динамическую структуру (рис. 3), ссылка на
которую передается между утилитами и приложением. Это уменьшает затрачиваемый
объем памяти и увеличивает быстродействие, но осложняет, в тоже время, технику
программирования: корректность заполнения и работы со структурой данных тела возлагается
на программиста. Стандартные структуры и подходы программирования высокого
уровня (массивы, записи, классы и объекты) позволяют контролировать данную
работу, но при большом количестве вершин и граней геометрического объекта
требуется высокая мощность компьютера. Вершины моделируемой конструкции являются
также узлами сетки, которые могут находиться как на границе кусочно-гладкой
поверхности, так и внутри нее. Положение узла может быть использовано в
процессе моделирования поверхности тела, для чего в данных задан признак
граничности: если узел лежит внутри дискретизированной поверхности – false,
иначе – true. Для визуального выделения узлов и граничных
элементов, в процессе интерактивного проектирования [2, 4] каждой вершине
и грани геометрического объекта задается цвет. Утилиты
проектирования. Все разработанные утилиты проектирования можно разбить на два типа: 1) утилиты генерации
гранично-элементной сетки – утилиты, которые моделируют сетку на конкретных конструкциях с
заданными параметрами. Например, это утилиты генерации гранично-элементной
сетки на поверхностях осесимметричных и блочных конструкций [1]. 2) утилиты проектирования
поверхностей твердых тел – утилиты, которые предназначены для моделирования поверхности
фундамента, представленной в виде гранично-элементной сетки, в диалоговом или
интерактивном режиме: · Утилита «редактор
многогранников», позволяющая добавлять, удалять или изменять координаты вершин
(узлов) геометрического объекта [4]. · Утилита дискретизации
макроэлементов, предназначенная для разбивки выбранных элементов
гранично-элементной сетки [2]. · Утилита моделирования
поверхности твердого тела с помощью логических композиций (объединения,
вычитания, пересечения) [3]. Утилиты
генерации гранично-элементной сетки. Основным требованием к разбиению контактной
поверхности на граничные элементы является отсутствие пересечений и перекрытий,
а точки на неплоской поверхности должны быть узлами смежных граничных
элементов. Разбиение в общем случае предполагается смешанным, то есть с одновременным
присутствием треугольных и четырехугольных граничных элементов. Используется глобальная
нумерация элементов с возможностью предпочтительного выделения определенной группы
элементов для удобства последующей обработки численных результатов. Локальная
нумерация узлов на каждом элементе всегда берется против часовой стрелки при
наблюдении со стороны внешней к контактной поверхности нормали. Для
всех типов поверхностей принята фрагментальная дискретизация, что соответствует
предварительному разбиению поверхности рассчитываемой конструкции на граничные
макроэлементы [1]. На следующем этапе производится разбиение граничных макроэлементов
на отдельные граничные элементы с автоматической генерацией координат и узлов.
В качестве граничных макроэлементов принимаются поверхностные фрагменты,
имеющие простейшую топологию. Как правило, это – плоские четырехугольники,
части цилиндрических, конических и сферических поверхностей. В отдельных
случаях используются граничные макроэлементы, уравнения поверхности которых
могут быть заданы детерминировано. Разбиение
граничных макроэлементов на отдельные граничные элементы производится регулярно
и не обязательно равномерно. Степень неравномерности разбиения в отдельном
граничном макроэлементе по различным направлениям задается параметрически и, по
возможности, учитывает предполагаемый характер изменения контактных напряжений. Важным
аспектом фрагментальной дискретизации является согласование по числу граничных
элементов на линиях сопряжения сложных граничных макроэлементов. Это необходимо
для улучшения численного решения и удобства при обработке и интерпретации
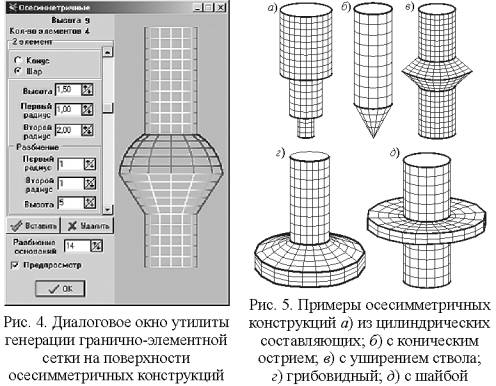
полученных результатов. Далее
рассмотрена дискретизация поверхностей конструкций осесимметричного (рис. 4, 5)
и блочного типа (рис. 6, 7). Осесимметричная
поверхность получается в результате вращения некоторой кривой вокруг оси
симметрии, в основном это прямая (конические или цилиндрические конструкции)
или окружность (сферические конструкции). Предполагается, что осью симметрии является
ось OZ. Полная дискретизация поверхности в виде тела вращения получается в
результате объединения граничных макроэлементов перечисленных выше простейших
форм. Исходя из физических представлений естественно ожидать, что поверхность,
аппроксимированная ансамблем плоских граничных элементов, будет немного отличаться
от реальной и что приближенное решение контактной задачи будет сходиться к
точному при малых размерах граничных элементов. Практические расчеты
показывают, что сходимость имеет место, причем достаточно хорошая [1]. На
основе приведенных методов разработана утилита генерации гранично-эелементных
сеток осесимметричных конструкций различных типов (рис. 4, 5).
Геометрия
каждого плоского граничного макроэлемента определяется заданием его вершин.
Разбиение граничных треугольных или четырехугольных макроэлементов на отдельные
элементы производим на основе техники изопараметрических элементов. Если на
стандартном квадрате взять равномерную или сгущающуюся к границе сетку элементов,
то линейное изопараметрическое преобразование переведет их в глобальные
граничные элементы без нарушения межэлементной непрерывности и с требуемой
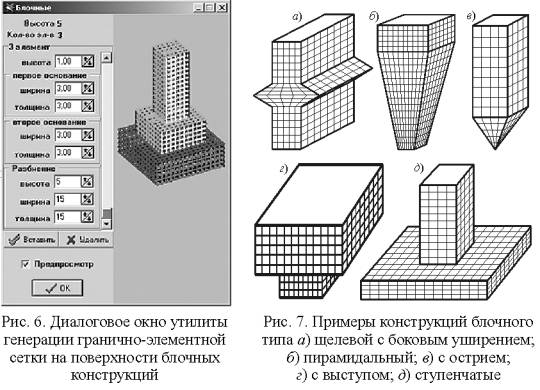
регулярной нумерацией узлов и вершин. На основе
данного подхода в программном модуле URAN разработана утилита генерации
пространственных сеток на конструкциях блочного типа (рис. 6, 7).
Утилита
корректировки гранично-элементной поверхности. Для возможности геометрического
моделирования и корректировки поверхности сложных конструкции в интерактивном режиме
разработана утилита редактирования
многогранников (рис. 8). Моделирование многогранника заключается в
добавлении, удалении и изменении координат вершин с учетом ориентации граней
(обход вершин грани с лицевой стороны против часовой стрелки).
При добавлении
вершины выделяются три вершины редактируемого многогранника, которые будут
связаны общими ребрами с добавляемой вершиной. Добавляемой вершиной может быть
как новая вершина, так и вершина многогранника, в последнем случае просто
добавляются ребра. Удаление вершины обратное добавлению: выделяются три смежных
вершины, и удаляются общие с удаляемой вершиной ребра. Таким образом,
осуществляется не само удаление, а «вырезание» пирамиды из редактируемого многогранника.
Алгоритмы редактора многогранников описаны в [4] Разработанные и реализованные в утилите
«редактор многогранников» алгоритмы позволяют генерировать модели поверхностей,
состоящих из плоских макроэлементов, которые разбиваются на треугольные и
четырехугольные макроэлементы утилитой дискретизации макроэлементов [2]. В
процессе дискретизации ищется такая гранично-элементная сетка, в которой
четырехугольные элементы были бы выпуклыми, а треугольные близки к равносторонним. Утилита построения гранично-элементных сеток
методом композиций. В современных САПр твердотельного моделирования распространен способ
построения конструкций со сложной топологией из композиций уже существующих или
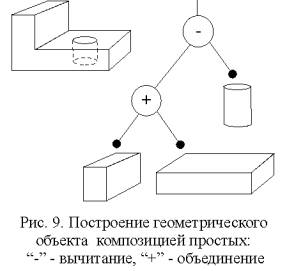
простых геометрических объектов (рис. 9).
Построение
гранично-элементных сеток методом композиций заключается в выделении граничных
элементов соответствующих решению и исключение пересечений и перекрытий.
Решение данной задачи основано на том факте, что операции композиций аналогичны
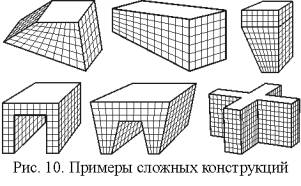
бинарным логическим операциям [3]. Заключение. Разработанные и реализованные утилиты
проектирования гранично-элементных сеток на поверхностях твердых тел позволяют
моделировать пространственные гранично-элементные сетки весьма сложной формы
(рис. 10) и характеризуются простой логической структурой и небольшими затратами
счетного времени. Существует возможность корректировки, сгущения и перестройки
существующих гранично-элементных сеток в процессе подготовки данных для
проектирования и инженерных расчетов.
Разработанная
система автоматизированного проектирования пространственных гранично-элементных
сеток является удобным средством подготовки данных (препроцессор) для решения
контактных задач. Существует возможность связи данного САПр гранично-элементных
сеток с существующими программными комплексами на уровне файлов данных,
разрабатывая и подключая соответствующие файловые утилиты. Программная реализация,
основанная на СОМ-технологии дает возможность интенсивному расширению и модификации
САПр гранично-элементных сеток путем разработки новых утилит проектирования.
Перечисленные свойства САПр гранично-элементных сеток позволяют без труда
адаптировать данный программный продукт под диапазон контактных задач, решаемых
методом граничных элементов, любого профиля и специальности. Список использованных источников 1.
Алейников С. М. Метод граничных элементов в контактных задачах для
упругих пространственно неоднородных оснований. – М.: Изд-во «АСВ», 2000. – 754
с. 2.
Алейников С. М.,
Вахтин А. А. Гранично-элементная дискретизация плоских областей в пространстве //
Информатика: проблемы, методология, технологии: Мат. IV рег. науч.-мет. конф.,
Воронеж: ВГУ, 2004. – С. 6-9. 3.
Алейников С. М.,
Вахтин А. А., Тюкачев Н. А. Алгоритмы построения пространственных гранично-элементных сеток //
Информатика: проблемы, методология, технологии: Мат. IV рег. науч.-мет. конф.,
Воронеж: ВГУ, 2004. – С. 9-11. 4.
Вахтин А. А.
Алгоритмы автоматического моделирования многогранников // Математическое
обеспечение ЭВМ: Межвуз. сб. научн. тр. Вып. 4., Воронеж: ВГУ, 2002. –
С. 27-31. 5.
Роджерсон Д. Основы COM. – М.: Русская Редакция, 2000. – 400 с. |
| Назад |
Материалы, опубликованные в данном сайте являются авторской интеллектуальной собственностью
и не могут быть использованы ни в каких целях и в никакой форме без письменного разрешения автора