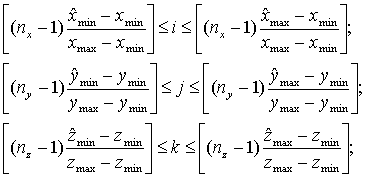| На главную |
| Структура программы |
| Презентация |
| Статьи |
| Контакты |
|
|

Обязательна ссылка на источник при использовании данных материалов
|
||||||||
Вахтин А. А. Метод композиций для гранично-элементной дискретизации. // Науч.-техн. журнал Системы управления и информационные технологии. - 2005. - № 4 (21) - С. 66 - 71. |
||||||||
| Назад | ||||||||
|
УДК 519.642:539.3:624.044:624.15 Метод
композиций для гранично-элементной Вахтин А. А. Воронежский государственный
университет, Аннотация. При решении
пространственных контактных задач теории упругости методом граничных элементов
возникают проблемы генерации гранично-элементной сетки на контактной
поверхности сложной формы. В работе предложен эффективный метод построения
пространственных гранично-элементных сеток методом композиций, используя пересечение,
вычитание и объединение гранично-элементных сеток простых поверхностей. Compose method for boundary
element Vahtin A. A. Voronezh State Univercity, Annotation. The solution space contact problem of theory of elasticity
by boundary element method has some problems building boundary element grid of
contact surface the intricate form. There is describe the proficient method
building space boundary element grid by composition method which use crossing,
subtraction or integration boundary element grid of simple surface. Введение.
Проблема разбиения контактных поверхностей остается актуальной, не смотря на
удобство предложенного в [1
] метода фрагментальной дискретизации, так как
некоторые контактные поверхности сложной формы весьма трудно разбить на
граничные макроэлементы. В современных САПР
твердотельного проектирования сложные конструкции представляются в виде
композиций [2
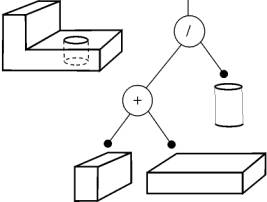
] простых геометрических объектов (рис. 1
). Данный метод можно использовать для построения гранично-элементных
сеток на поверхностях рассчитываемых конструкций, состоящих из фрагментов,
разбиение которых тривиально или уже известно. Основная идея
рассматриваемого метода композиций заключается в представлении декартового
пространства как множество, где операции сложения, вычитания и пересечения
соответствуют построению поверхностей геометрических объектов.
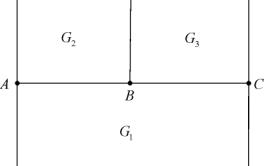
рис. 1.
Построение геометрического объекта композицией простых: Разработанный метод
композиций рассчитан только для замкнутых поверхностей. Определение 1. Поверхность
Проверка гранично-элементных сеток на замкнутость. Для того чтобы поверхность, аппроксимированная граничными элементами, была замкнута, необходимо чтобы ребра граничных элементов принадлежали не менее двум граничным элементам. Более того, ребро не может принадлежать более двум граничным элементам, так как это нарушает целостность фигуры [3 – 5]. Так как обход узлов
граничных элементов ориентирован, то по ребру
рис. 2. Обход узлов в ребре граничных элементов В соответствии с данными
условиями, для проверки на замкнутость удобно использовать представление
гранично-элементной сетки в виде графа, реализованного в программе как матрица
целых чисел Приведение
гранично-элементной сетки к замкнутому виду. Из условий контактных задач [1
] следует, что для решений используются не замкнутые
поверхности. Но это не ограничивает применение метода композиций, так как любую
не замкнутую поверхность можно привести к замкнутой путем добавления новых
граничных элементов и удалением их непосредственно перед расчетом. Если существуют элементы
матрицы В итоге получаются плоскости,
покрывающие грани из В некоторых случаях могут быть
добавлены поверхностные фрагменты с нулевой площадью, чтобы исключить
односторонний проход по соответствующим ребрам. Например, для случая
представленного на рис.
3 нужно добавить граничный элемент
рис. 3. Узел Метод композиций. Пусть заданы замкнутые
поверхности n геометрических объектов Утверждение 1. Каждому множеству
Доказательство. Иcпользуя метод математической
индукции легко доказать, что n множеств, в общем случае,
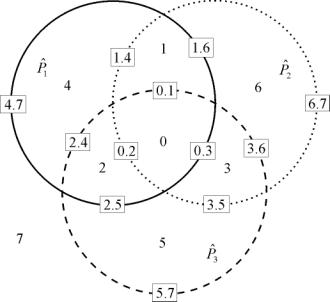
разбивает множество Для двух множеств табл. 1. Нумерация подмножеств
Пусть данное утверждение
верно для всех Остается найти двоичные коды
множеств и доказать, что они удовлетворяют данному утверждению. Пусть заданы
множества Так как операции над множествами коммутативны, ассоциативны и дистрибутивны [6], то любое выражение можно представить в следующем виде: Иными словами, вычисление
выражений над множествами Если принять замену Например, для трех множеств
(рис. 4
) будут соответствовать следующие коды:
рис. 4. Нумерация подмножеств и границ для трех множеств Следует заметить, что
двоичные коды множеств обладают важным свойством: пары различных битов кода
множества соответствуют границе множества. Иными словами, индексы граничных
элементов будут совпадать с парой номеров различных битов в двоичном
представлении кода операции, если: 1)
каждому
граничному элементу геометрических объектов сопоставить индекс, состоящий из
номеров подмножеств, которые они разделяют: 2)
каждой
паре различных битов в двоичном представлении множества сопоставить индексы В случае, когда Например, в выражении Данный алгоритм позволяет без труда вычислять любые операции композиций над любым числом геометрических объектов, выделять граничные элементы, соответствующие искомому решению и учитывать локальную нумерацию вершин (обход против часовой стрелки, если смотреть с внешней стороны), что весьма важно при использовании метода граничных элементов. Нумерация граничных элементов. Критерием нумерации граничных элементов является определение пространственного положения каждого граничного элемента (рис. 4 ). Естественно, при классификации необходимо исключить пересечения граничных элементов с поверхностью геометрического объекта разбиением их на части. Определение 2. Если граничный элемент геометрического объекта находится внутри области, ограниченной замкнутой поверхностью, то он называется внутренним, если вне области – внешним. Пусть поверхности
геометрических объектов замкнуты и аппроксимированы набором граничных
элементов, которые не пересекаются друг с другом. Тогда для выполнения критерия
нумерации достаточно определить пространственное положение узлов: у внутреннего граничного элемента все узлы находятся внутри области или на
поверхности геометрического объекта, у внешнего – узлы расположены вне области.
Данное допущение не ограничивает общность алгоритма, так как
гранично-элементная сетка для контактных задач теории упругости состоит
из набора плоских (в основном треугольных и четырехугольных элементов), которые
легко подвергаются дискретизации на элементы меньшего размера [1
]. Алгоритм определения
пространственного положения узлов основан на методе трассировки лучей [5
]. Пусть задана некоторая точка Если n четно, то M –
находится вне области, ограниченной рассматриваемой гранично-элементной сеткой,
иначе – внутри. При реализации данного алгоритма следует учесть
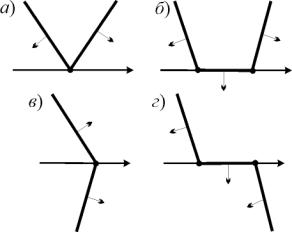
некоторые особенности при пересечении лучом
рис. 5. Типы пересечений лучом с
гранично-элементной сеткой в ребрах Пусть луч После нумерации граничных элементов
можно вычислить любые операции композиций в соответствии с полученными
двоичными кодами множеств. Хеш-таблица для граничных элементов. В алгоритме нумерации
гранично-элементных сеток необходимо рассматривать пересечения граничных
элементов с лучом . Ввиду большого объема данных, полный перебор не эффективен, так как
существенно замедляет работу алгоритма. Появляется необходимость отбросить
большую часть граничных элементов, которые не могли бы пересекаться с лучом,
выпущенным из заданной точки и параллельным оси Чтобы построить хеш-таблицу
для граничных элементов, нужно рассмотреть задачу поиска пересечений граничных
элементов и луча геометрически. Утверждение 2. Если для вершин плоского многоугольника выполняются неравенства то они выполняются для всех точек данного многоугольника. Доказательство. Пусть неравенства
выполняются для вершин многоугольника Без ограничения общности
можно предположить, что Аналогичные рассуждения
применимы и для остальных случаев, когда для точек многоугольника Из данного утверждения следует: 1.
Для
того, чтобы луч пересекал граничный элемент, необходимо, чтобы для координат точки, из
которой выпущен заданный луч выполнялись следующие неравенства: где 2.
Если
для узлов гранично-элементной сетки выполняются неравенства , то для любой точки гранично-элементной сетки, тоже будет выполняться
данное неравенство; Для доказательства первого
следствия достаточно рассмотреть геометрическое свойство луча и что если луч пересекает граничный элемент, то хотя бы одна из точек
луча будет принадлежать данному граничному элементу, для координат которой
будут выполняться неравенства . В качестве доказательства второго следствия достаточно рассмотреть сетку как набор граничных элементов, геометрически являющихся многоугольниками: так как для них выполнима теорема о неравенствах, то она и выполнима для множества точек данных граничных элементов, следовательно, и для всей сетки в целом. Таким образом, можно найти
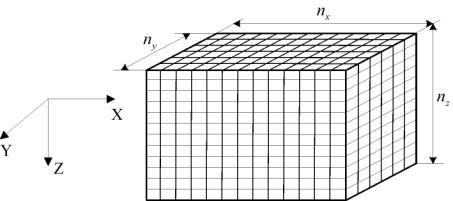
такие минимальные и максимальные значения координат, чтобы гранично-элементная
сетка была заключена в параллелепипед, представленный в виде неравенств
. Полученный параллелепипед можно разделить на
рис. 6. Разбиение прямоугольного параллелепипеда,
охватывающего Каждому множеству узлов,
заданных неравенствами можно задать индекс: где
Из второго следствия теоремы
о неравенствах очевидно, что пространственная точка может быть внутри области,
ограниченной гранично-элементной сеткой, только тогда, когда для координат
данной точки выполняются неравенства . Следовательно, подсчет числа пересечений с лучом имеет смысл только для координат точек множества , для которых можно применять хеш-функцию . Используя неравенства
, и функцию можно получить индексы множеств точек, для которых существует
вероятность пересечения луча с граничным элементом сетки:
где
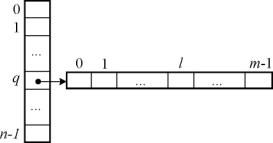
рис. 7. Структура хеш-таблицы: элементы хранятся в массивах переменной длинны Очевидно, что информация,
хранимая в построенной хеш-таблице избыточна, но это компенсируется
возможностью для любой пространственной точки весьма быстро отбросить существенное
количество не нужных граничных элементов и выделить только те, которые могут
пересекаться с лучом . Практический опыт показал, что разработанная хеш-таблица для
граничных элементов существенно сокращает время выполнения метода композиций. Заключение.
Разработанный алгоритм построения пространственных гранично-элементных сеток методом
композиций состоит из следующих этапов: 1) проверка
гранично-элементной сетки на замкнутость и в случае необходимости добавление
граничных элементов; 2) в
соответствии с установленной нумерацией граничные элементы разделяются на 3) вычисляется
двоичный код, соответствующий решению метода композиций; 4) в
зависимости от пар несовпадающих битов в полученном двоичном коде выделяются
необходимые узлы и граничные элементы. На основе предложенных алгоритмов в препроцессоре
гранично-элементного программного комплекса [7
] разработана соответствующая утилита построения
гранично-элементных сеток сложной формы Метод композиций характерен простотой реализацией и
позволяет быстро определять искомое решение, что весьма необходимо не только в
задачах простого проведения расчета деформаций оснований сложных конструкций,
но и для реализации поиска оптимальных решений путем изменения геометрической
формы рассматриваемой конструкции поворотом или перемещением простых
геометрических объектов в пространстве. Список использованных источников 1.
Алейников С. М. Метод граничных элементов в контактных задачах для упругих пространственно
неоднородных оснований. – М.: АСВ, 2000.– 754 с. 2.
Райан Д. Инженерная графика в САПР:
пер. с англ. – М.: Мир, 1989. – 3.
Корнишин М. С., Паймушин В. Н., Снигирев
В. Ф. Вычислительная геометрия в задачах механики оболочек. – М.: Наука,
1989. – 208 с. 4.
Ласло М. Вычислительная геометрия и
компьютерная графика на С++: пер. с англ. – М.: БИНОМ, 1997. – 304 с. 5.
Роджерс Д., Адамс Дж.
Математические основы машинной графики: пер. с англ. – М.: Мир, 2001. – 604 с. 6.
Хаусдорф Ф. Теория множеств: пер. с
нем. – М.: УРСС, 2004. – 304 с. 7.
Вахтин А. А. Препроцессор
гранично-элементного программного комплекса для решения задач геотехники. //
Науч.-техн. журнал Системы управления и информационные технологии. – 2003. – №
1-2 (12) – С. 68 – 72. |
||||||||
| Назад |
Материалы, опубликованные в данном сайте являются авторской интеллектуальной собственностью
и не могут быть использованы ни в каких целях и в никакой форме без письменного разрешения автора

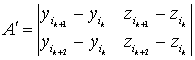 ,
, 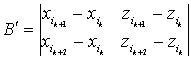 ,
, 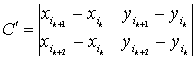 .
.
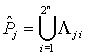 , где
, где 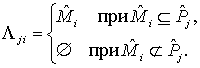
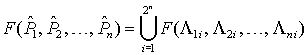 .
.
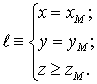
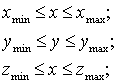
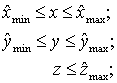
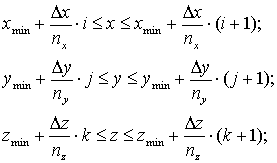
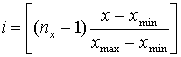 ,
, 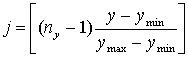 ,
, 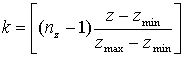 ,
,