УДК 519.642:539.3:624.044:624.15

Методы корректировки пространственной
гранично-элементной сетки

Вахтин А. А.

Воронежский государственный университет,
e-mail: wishmaster_79@mail.ru

 

Аннотация. Рассматриваются алгоритмы построения пространственной гранично-элементной сетки путем добавления или удаления узлов и граничных элементов. Предложенные алгоритмы позволяют получать гранично-элементную дискретизацию поверхностей любой сложности интерактивным полуавтоматическим методом.

 

The methods of adjust of space boundary element grid

Vahtin A. A.

Voronezh State Univercity,
e-mail: wishmaster_79@mail.ru

 

Annotation. There is describing the algorithms of building space boundary element grid by addition or removal points or boundary elements. This algorithms are designed for getting boundary element grid different intricate with interactive assisted method.

 

УДК 519.642:539.3:624.044:624.15

Вахтин А. А.

Методы корректировки пространственной
гранично-элементной сетки

Воронежский государственный университет

 

Введение. Применение метода граничных элементов для численного моделирования процессов контактного взаимодействия в теории упругости требует нанесения на контактную поверхность гранично-элементной сетки, от качества которой во многом зависит получаемое численное решение [1].

Для построения гранично-элементной сетки, состоящей из плоских многоугольных фрагментов, в интерактивном полуавтоматическом режиме разработаны алгоритмы, основанные на геометрическом построении поверхности:

1)     пространственное перемещение вершин;

2)     добавление новых вершин и граней;

3)     удаление вершин и граней.

Без ограничения общности можно считать граничные элементы сетки гранями, а узлы – вершинами. Поверхность, образованная набором граней в дальнейшем будет называться граничной.

Для однозначности построений грани с общим ребром и лежащие в одной плоскости объединяются, а по завершении полученные плоские фрагменты разбиваются на треугольные и четырехугольные элементы в соответствии с необходимыми требованиями [1].

При реализации алгоритмов необходимо соблюдать правило локальной нумерации вершин в гранях: против часовой стрелки при наблюдении с внешней стороны поверхности. В дальнейшем данное правило будет называться ориентацией граней.

После построения полученную поверхность необходимо проверять на правильность (отсутствие пересечений и перекрытий) и в случае ошибки предоставить возможность вернуться к предыдущим результатам.

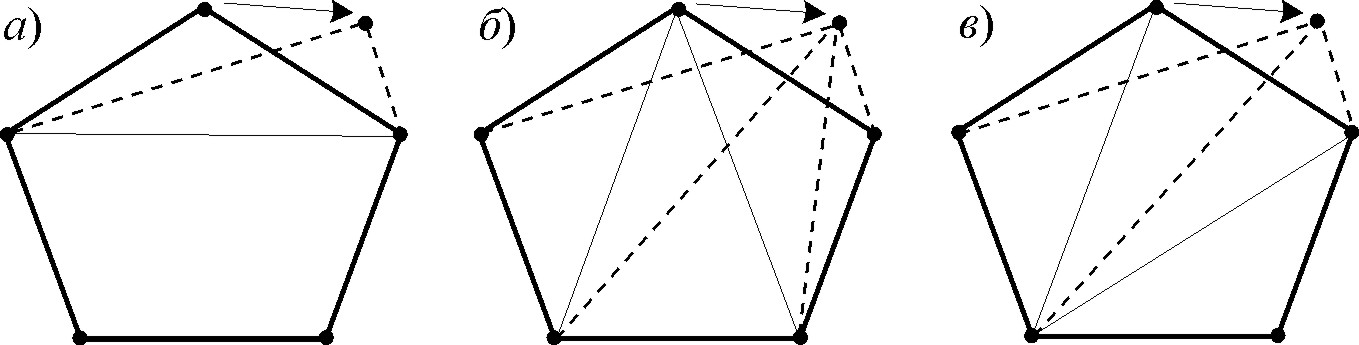
Пространственное перемещение вершин. Если вершина принадлежит только треугольным граням, то изменение ее координат не составит труда: три точки всегда будут лежать на плоскости. В не треугольной грани перемещаемая вершина может оказаться вне плоскости, образованной другими вершинами. Для решения данной проблемы применяется триангуляция грани, которая может быть не однозначна (рис. 1).

 

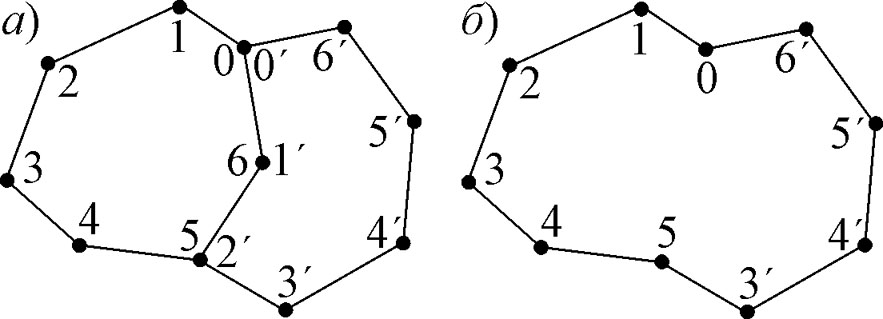
рис. 1. Всевозможные разбиения пятиугольной грани при пространственном перемещении узла: а) на две части б) в) на три части

 

Как показал практический опыт в методе перемещения вершин достаточно иметь только один вариант триангуляции грани, так как остальные можно получить за конечное число геометрических преобразований (добавление или удаление узлов и граней). Для однозначности построений используется отсечение треугольного элемента (рис. 1, а), а если это не возможно, грань предварительно разбивается на треугольные части по хордам (рис. 2), что по теореме о триангуляции полигонов [2] возможно всегда.

 

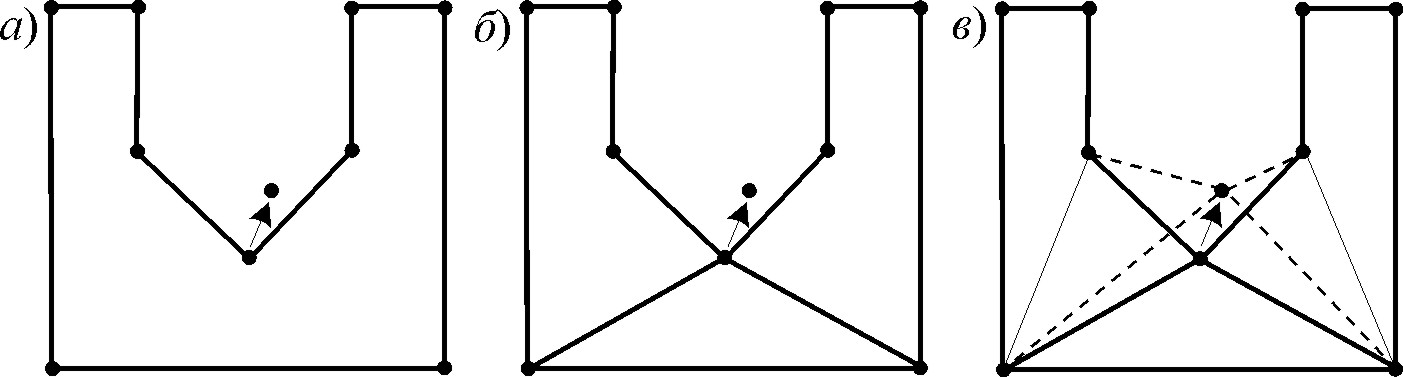
рис. 2. Разбиение грани при переносе вершины не выпуклого угла: а) исходная грань; б) предварительное разбиение грани на части; в) отсечение треугольных элементов и перенос вершины

 

Добавление новых вершин и граней. Добавление нового узла заключается в построении новых ребер и граней, соединяющих заданную пространственную точку с вершинами граничной поверхности. При реализации данной операции необходимо определять ориентацию добавляемых граней, которая зависит от обхода узлов в смежных гранях (рис. 3).

 

рис. 3. Обход узлов в ребре граничных элементов

 

Таким образом, для добавления узла необходимо:

1)     зафиксировать вершины граничной поверхности;

2)     определить обход фиксированных вершин (называется контуром);

3)     построить грани, связанные с узлами контура и новой вершиной;

4)     определить и удалить фрагменты, ограниченные контуром и новыми гранями.

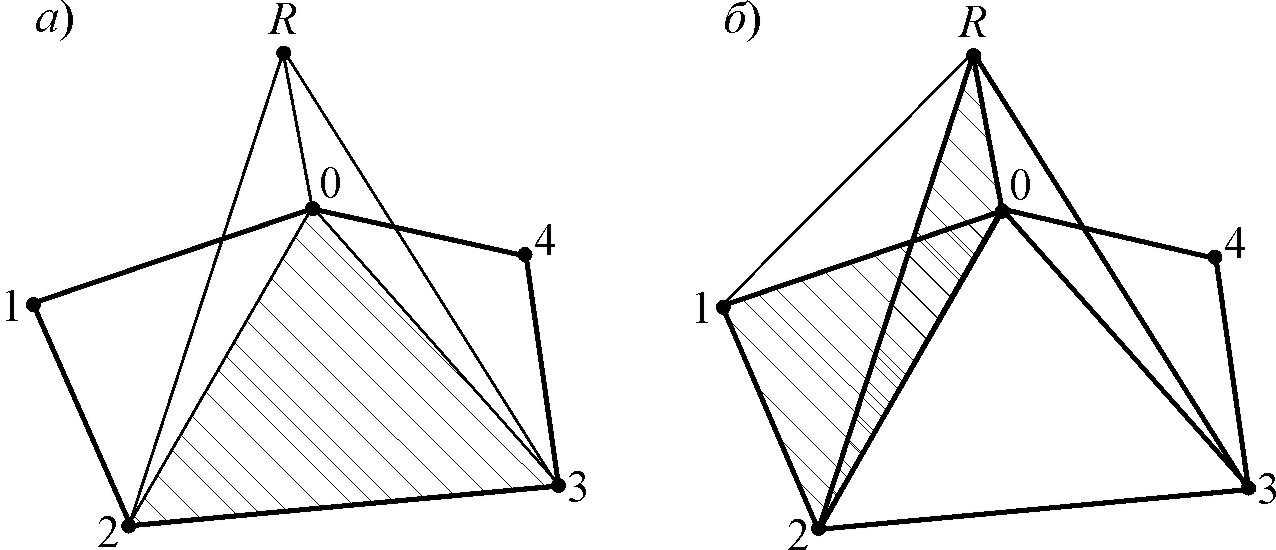
Для однозначности решения поставленной задачи решено фиксировать только три вершины лежащие на одной грани. Данное упрощение не ограничивает возможности геометрического построения, так как любое решение может быть достигнуто за конечное число геометрических преобразований.

На рис. 4, а изображен пример добавления новой вершины R, которая соединяется с вершинами 0, 2 и 3. В соответствии с обходом вершин выделяется контур [3, 2, 0] и строятся новые грани: [0, 2, R], [2, 3, R] и [3, 0, R]. Грань [0, 1, 2, 3, 4] разбивается на части с целью выделения и удаления фрагмента, образованного вершинами 0, 2, 3.

 

рис. 4. Добавление новой (а) и существующей (б) вершины R к граничной поверхности (штриховкой отмечены удаляемые фрагменты)

 

Данный алгоритм позволяет добавлять не только новые вершины, но и новые грани, если свободной точкой будет вершина граничной поверхности (рис. 4, б).

Удаление вершин и граней. Сложность удаления вершины заключается в том, что если у удаляемой вершины имеется четыре или более соседних вершин не лежащих в одной плоскости, то это приводит к неоднозначности в создании новых граней, а значит – к различным вариантам результата удаления. Поэтому разработано не само удаление, а отсечение части многогранника, выделенного четырьмя смежными вершинами (далее называемые фиксированными). Это позволяет не только сохранить единственность решения и удалить намеченную вершину за конечное число шагов, но и предусмотреть удаление граней и ребер.

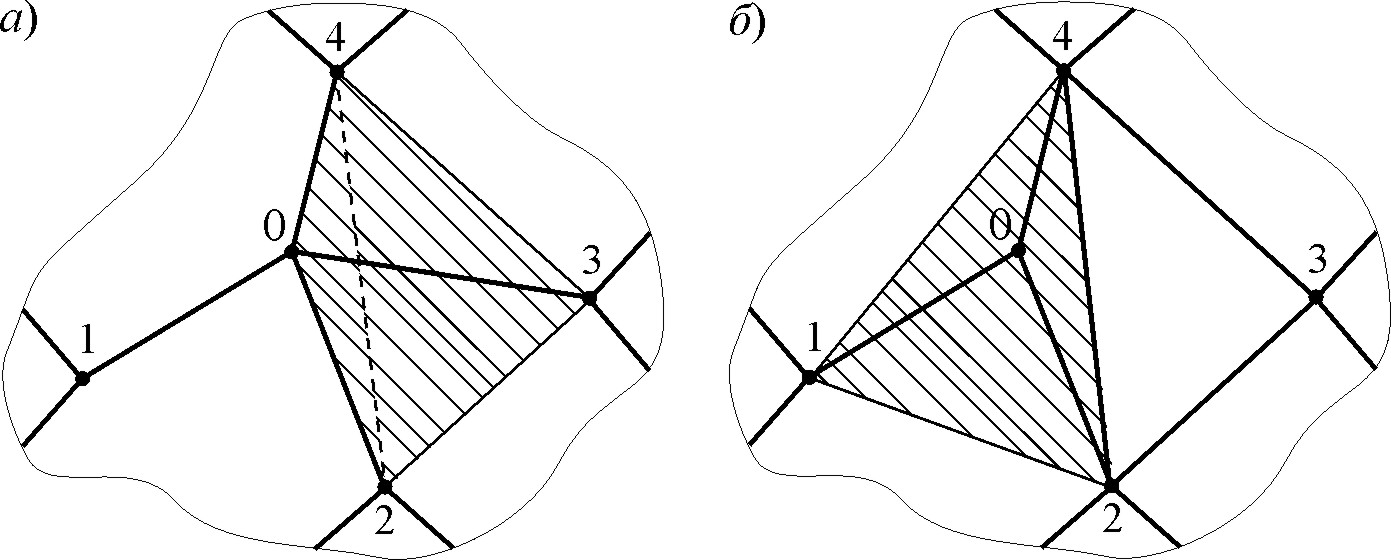
Без ограничения общности считается, что существует такая грань, которой принадлежат три фиксированных вершины. Данная грань позволяет определить ориентацию добавляемых граней (рис. 3). Это следует из геометрической структуры граничной поверхности [2].

Например, для удаления вершины 0 связанной с вершинами 1, 2, 3, 4 необходимо вырезать фрагменты [0, 3, 4] и [0, 2, 3] (рис. 5, а), а затем удалить полностью (рис. 5, б).

 

рис. 5. Выполнение процедуры удаления узла 0 (штриховкой отмечены добавляемые фрагменты): а) отсечение фрагментов; б) удаление полностью

 

Проверка граничной поверхности на правильность. Предложенные алгоритмы исключают возможность перекрытий и нарушение правила обхода узлов (ориентация граней), если корректируемая поверхность изначально имела правильную структуру, но на каждом шаге построения требуется проверять связность поверхности и отсутствие пересечений граней.

 

Определение 1. Поверхность  называется связной, если для любых двух точек  существует непрерывная кривая, соединяющая данные точки и полностью принадлежавшая .

 

Так как любые две точки любой грани рассматриваемой поверхности можно соединить кривой, то для критерия связности достаточно рассмотреть вершины и ребра.

 

Утверждение 1. Поверхность , состоящая из набора плоских многоугольников, является связной тогда и только тогда, когда для любых двух вершин данной поверхности, существует цепочка ребер, соединяющая их.

Доказательство.

1) Требуется доказать, что если поверхность  является связной, то любые две вершины, можно соединить цепочкой ребер.

Пусть заданы любые две вершины. Требуется найти соответствующую цепочку ребер, соединяющую их. По определению связности данные вершины можно соединить кривой , принадлежащей . Тогда кривая  будет пересекать или проходить по ребрам граней поверхности . Без ограничения общности определения связности точки пересечений ребер в гранях можно соединить кривой, проходящей по ребрам. В таком случае можно построить кривую, проходящую по ребрам поверхности , которая и будет искомой цепочкой. Так как данные две вершины любые, теорема доказана.

2) Требуется доказать, что если любые две вершины можно соединить цепочкой ребер, то поверхность  связная.

Так как грани поверхности  тоже являются связными, то любые точки данной грани можно соединить с вершинами, которые, по условию, можно соединить цепочкой ребер. Следовательно, для любой точки поверхности  можно построить непрерывную кривую, соединяющую данные точки, тогда  является связной по определению, что и требовалось доказать.

 

Алгоритм определения связности граничной поверхности основан на представлении граничной поверхности в виде графа [3], где вершины поверхности являются узлами, а ребра – дугами. Очевидно, что если для одной вершины можно найти путь, проходящий по ребрам, до всех вершин, то можно найти соответствующий путь между любыми вершинами (например, проходящий через данную точку).

Для выявления пересечений двух граней используется критерий, сформулированные в виде теоремы 2.

 

Утверждение 2. Две грани пересекаются, если их вершины лежат в разных полупространствах, разделяемых плоскостями данных граней.

Доказательство.

Для доказательства данной теоремы достаточно провести прямую  на пересечении двух плоскостей заданных граней. Грань будет разделена прямой , если ее вершины лежат в разных полупространствах, разделяемых плоскостью другой грани. Тогда если вершины двух граней будут находиться в разных полупространствах, то данные грани будут иметь общие точки, принадлежащие прямой . Следовательно, они будут пересекаться, что и требовалось доказать.

 

Чтобы определить пространственное положение точки  достаточно определить знак выражения

,        

где A, B, C и D – коэффициенты уравнения плоскости в нормальном виде.

Если для вершин грани выражения разного знака, то они находятся в разных полупространствах, ограниченных плоскостью, заданной данным уравнением.

Объединение граней. После операций перемещения, добавления или удаления вершины требуется объединение граней, лежащих в одной плоскости и имеющих общие ребра. Иными словами, строится новая ориентированная грань, содержащая все ребра исходных (рис. 6).

 

рис. 6. Объединение граней: а) до операции; б) после

 

При объединении двух граней последовательность вершин первой грани включается в новую. Если встретится общий узел, то обход вершин продолжается на следующем граничном элементе до тех пор, пока последовательность не замкнется в вершине, с которой был начат обход. Следует заметить, что данный алгоритм необходимо всегда начинать с не общей вершины, так как в противном случае можно получить неверное решение. На рис. 6 рассмотрен пример интеграции граней [0, 1, 2, 3, 4, 5, 6,] и [0´, 1´, 2´, 3´, 4´, 5´, 6´].

Во время редактирования приходится не только объединять граничные элементы, но и вычитать, если их лицевые стороны противоположны. Данный алгоритм предусматривает и этот случай.

Дискретизация граней. При построении гранично-элементной сетки требуется разбиение плоских фрагментов на треугольные и четырехугольные элементы в соответствии с требованиями к гранично-элементной сетке для контактных задач.

В [1] предложено применение алгоритма триангуляции двумерных областей для дискретизации фрагментов произвольной формы разбиением их на полосы, которые, в свою очередь, подвергаются триангуляции. Но применение данной триангуляции в гранично-элементных сетках неэффективно, так как это отражается на точности численного решения поверхностных интегралов и расположение центров масс (узлов коллокаций), которые, по условию численной реализации контактных задач равномерно распределяются по контактной поверхности.

Наиболее оптимальным вариантом дискретизации плоских макроэлементов произвольной формы разработан алгоритм, основанный на доказанной в [2] теореме о триангуляции полигона: n-угольник может быть разбит на  треугольника проведением  хорд. Следовательно, плоский фрагмент произвольной формы можно разбить по хордам на треугольные и выпуклые четырехугольные фрагменты, для которых применимы формулы аппроксимации [1].

При разбиении фрагмента выбираются хорды, выпущенные из больших углов, чтобы получаемые четырехугольные фрагменты были близки к прямоугольным, а треугольные к равносторонним.

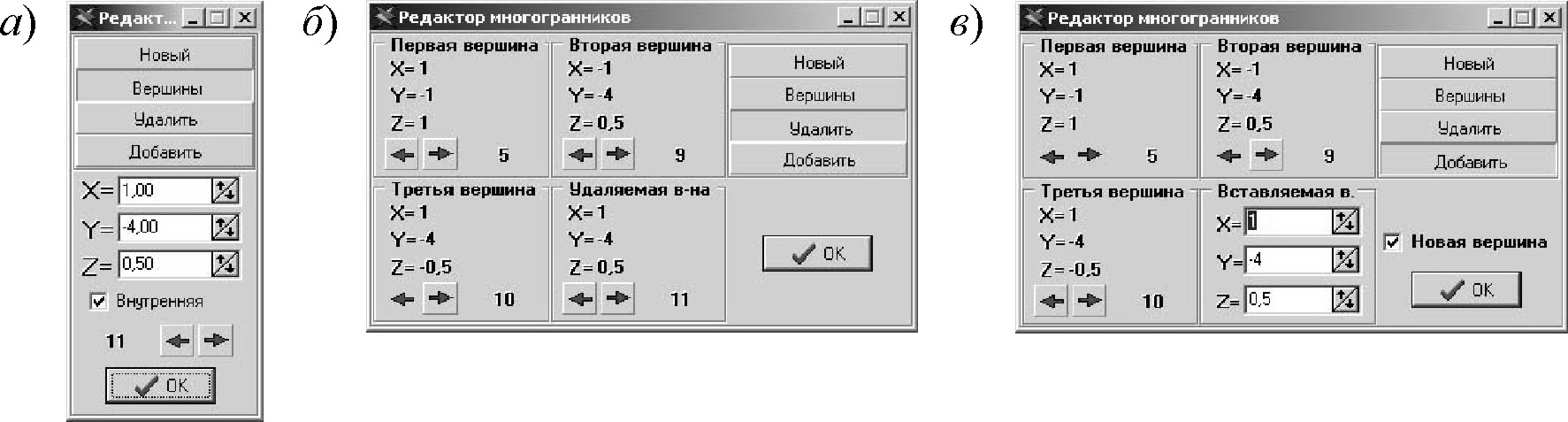
Заключение. На основе предложенных методов в препроцессоре гранично-элементного программного комплекса для решения задач геотехники [4] разработана утилита редактор многогранников, в которой реализованы методы пространственного перемещения, удаления и добавления вершин (рис. 7).

 

рис. 7. Диалоговое окно редактора многогранников в режиме
а) изменения координат; б) удаления; в) добавления

 

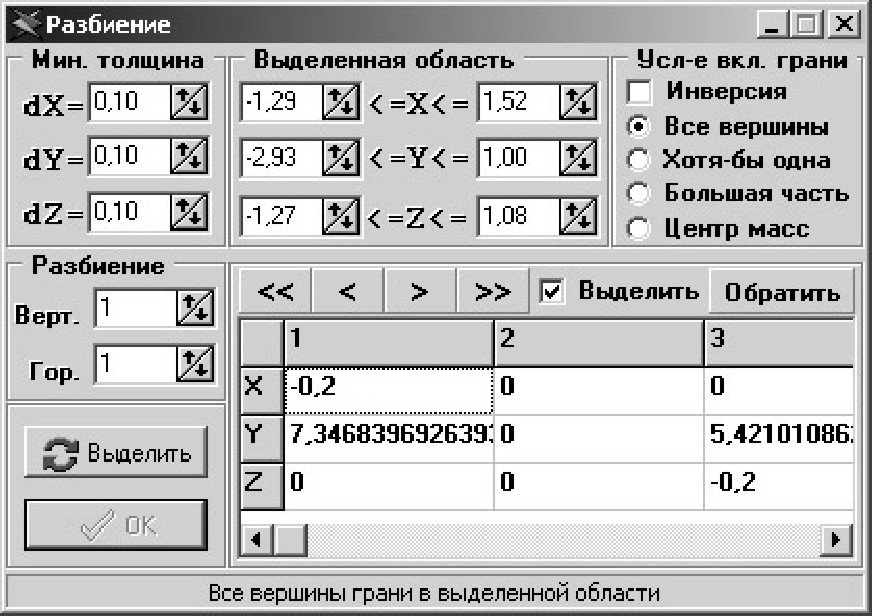
Дискретизация поверхностных фрагментов применяется как при построении гранично-элементной сетки, так и для более мелкого разбиения граничных элементов при решении контактных задач (например, при учете больших изменений функции контактных напряжений). Для этих целей в препроцессоре [4] используется утилита дискретизации плоских фрагментов (рис. 8).

Подвергаемые дискретизации поверхностные фрагменты можно выбрать как вручную мышью в окнах проекций препроцессора [4] или в блоке навигаций диалогового окна утилиты дискретизации (рис. 8), так и автоматически, включая все элементы, попадающие в заданный прямоугольный параллелепипед. Выделенные фрагменты разбиваются на треугольные и четырехугольные элементы, которые затем разбиваются по формулам аппроксимации [1].

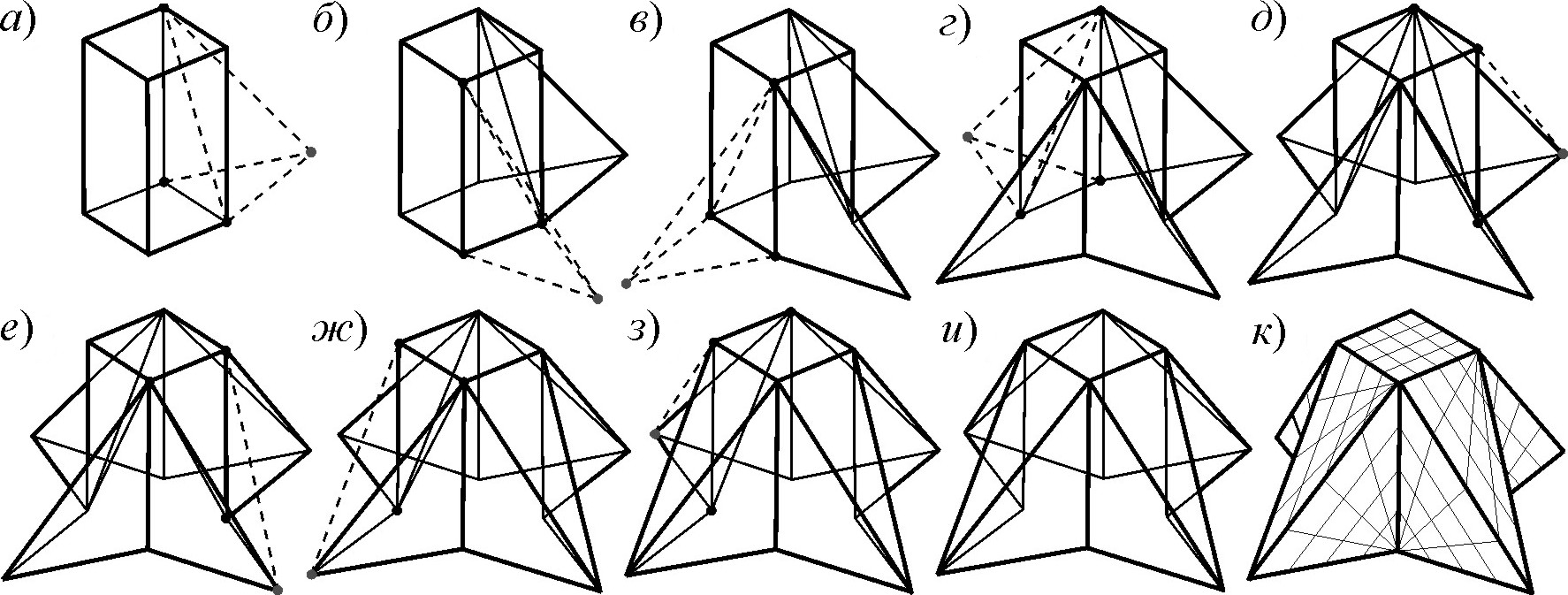
рис. 8. Утилита дискретизации плоских фрагментов

 

На рис. 9 (а – и) приведен пример построения поверхности щелевой крестообразной конструкции с наклонными боковыми гранями с помощью добавления вершин. После построений полученная поверхность разбивается на граничные элементы (рис. 9, к).

 

рис. 9. Построение поверхности щелевой крестообразной конструкции
с наклонными боковыми гранями с помощью добавления вершин
в интерактивном режиме

 

Разработанные алгоритмы предоставляют возможность построения гранично-элементных сеток любой сложности путем геометрической модификации существующих и проводить дискретизацию поверхностей, аппроксимированных плоскими фрагментами, для получения необходимой степени густоты.

 

Список использованных источников

1.     Алейников С. М. Метод граничных элементов в контактных задачах для упругих пространственно неоднородных оснований. – М.: АСВ, 2000.– 754 с.

2.     Ласло М. Вычислительная геометрия и компьютерная графика на С++: пер. с англ. – М.: БИНОМ, 1997. – 304 с.

3.     Берж К. Теория графов и ее применения: пер. с французского. – М.: изд-во иностранной литературы, 1962. – 320 с.

4.     Вахтин А. А. Препроцессор гранично-элементного программного комплекса для решения задач геотехники. // Науч.-техн. журнал Системы управления и информационные технологии. – 2003. – № 1-2 (12) – С. 68 – 72.