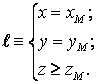| На главную |
| Структура программы |
| Презентация |
| Статьи |
| Контакты |
|
|

Обязательна ссылка на источник при использовании данных материалов
|
Вахтин А.А. Хеш-таблицы для сокращения времени выполнения алгоритма построения гранично-элементных сеток методом композиций. // Черноземный альманах научных исследований. - 2006. - Вып. 1 (2), С. 71-81. |
| Назад |
|
УДК
519.642:539.3:624.044:624.15 Вахтин А. А. Хеш-таблицы для
сокращения времени выполнения алгоритма построения гранично-элементных сеток
методом композиций Воронежский
государственный университет ВВЕДЕНИЕ При реализации некоторых алгоритмов построения гранично-элементной сетки необходим
поиск узлов или пересечений граничных элементов с геометрическими объектами (граничным
элементом, лучом, плоскостью, поверхностями и т. п.) [1, 2]. Одним из наиболее эффективных способов реализации быстрого поиска является
применение метода хеширования данных, что позволяет сократить среднее
время поиска элемента до порядка МЕТОД КОМПОЗИЦИЙ Для построения хеш-таблиц
узлов и граничных элементов необходимо выяснить их цель и практическую
необходимость. В качестве примера рассмотрим алгоритм метода композиций,
реализация которого подробно рассмотрена в [2]. Основная идея метода композиций заключается в представлении
декартового пространства как множество, где операции сложения, вычитания и
пересечения соответствуют построению поверхностей геометрических объектов. Таким образом, замкнутые
поверхности n геометрических объектов Алгоритм данного метода основан на утверждении, что каждому
множеству Методом математической
индукции можно доказать, что n множеств, в общем случае, разбивает множество Найдем двоичные коды
множеств. Пусть заданы множества Так как подмножества Иными словами, вычисление
выражений над множествами Если принять замену Например, для трех
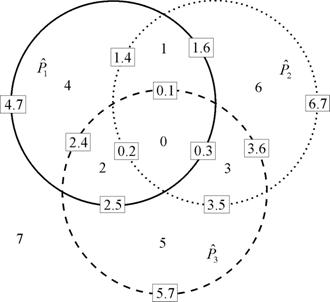
множеств (рис. 1) будут соответствовать следующие коды: Двоичные коды множеств
обладают важным свойством: пары различных битов кода множества соответствуют
границе множества. Иными словами, индексы граничных элементов будут совпадать с
парой номеров различных битов в двоичном представлении кода операции, если: 1) каждому граничному элементу
геометрических объектов сопоставить индекс, состоящий из номеров подмножеств,
которые они разделяют: 2) каждой паре различных битов в
двоичном представлении множества сопоставить индексы В случае, когда
Рис. 1. Нумерация подмножеств и
границ для трех множеств Например, в выражении Таким образом, двоичные коды позволяют без труда вычислять любые операции
композиций над любым числом геометрических объектов, выделять граничные
элементы, соответствующие искомому решению и учитывать локальную нумерацию
вершин (обход против часовой стрелки, если смотреть с внешней стороны), что
весьма важно при использовании метода граничных элементов. Критерием
нумерации граничных элементов является определение пространственного положения
каждого граничного элемента. Если граничный элемент геометрического объекта
находится внутри области, ограниченной замкнутой поверхностью, то он называется
внутренним, если вне области – внешним [2]. Пусть поверхности геометрических объектов аппроксимированы набором
граничных элементов таким образом, что гранично-элементные сетки пересекаются
по ребрам. Иначе необходимо разбить
граничные элементы, которые пересекаются с другой поверхностью так, чтобы
исключить пересечение. В таком случае, чтобы определить пространственное
положение граничного элемента, достаточно рассмотреть пространственное
положение любой его точки (например, вершины или центра масс). Алгоритм определения пространственного положения фиксированной
точки основан на методе трассировки лучей [4]. Пусть n – число пересечений поверхности
Если n четно, то M – находится вне области, ограниченной рассматриваемой
гранично-элементной сеткой, иначе – внутри. Следует заметить, что при реализации данного алгоритма следует учесть возможность
пересечений луча (3) с сеткой в узлах, ребрах или по плоскости граничного элемента.
Реализация алгоритма со всевозможными вариантами рассмотрена в [2] и здесь
рассматриваться не будет. Таким образом, при реализации алгоритма метода
композиций необходимо реализовать поиск граничных элементов, которые
пересекаются с – поверхностью (гранично-элементной сеткой)
другого геометрического объекта; – лучом (3) выпущенным из заданной точки
граничного элемента. Очевидно, что метод полного перебора для большого
числа граничных элементов не эффективен. Необходимо реализовать возможность
отбросить существенную часть граничных элементов, которые явно не имеют
пересечений. ХЕШ-ТАБЛИЦЫ
ДЛЯ УЗЛОВ Поиск индекса узла с
соответствующими координатами необходим для индексации вершин граничных
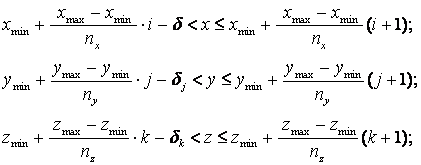
элементов. Пусть заданы такие Отрезки (1) можно
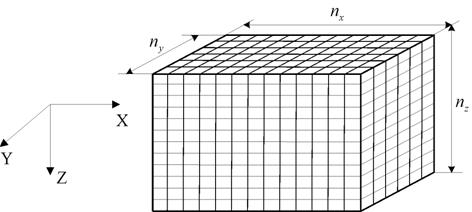
разделить на где
Рис. 2. Разбиение прямоугольного
параллелепипеда, охватывающего узлы гранично-элементной сетки, на Каждому множеству узлов,
заданных неравенствами (5) можно задать индекс: Из формул (5) и (6) можно
получить хеш-функцию для хеш-таблицы объемом Чтобы получить
хеш-функцию для любых узлов достаточно взять остаток от деления (7) на объем
таблицы Узлы с одинаковыми
хеш-индексами можно хранить в списке или открытом
массиве. Следует заметить, что равномерность заполнения ячеек хеш-таблицы
зависит от распределения узлов гранично-элементной сетки в контактной поверхности.
Таким образом, можно получить хеш-таблицу для узлов гранично-элементной сетки,
с хеш-функцией (7), позволяющей равномерно разбить узлы сетки на множества
меньшего размера ( Хеш-таблица для узлов
применима не только в методе композиций, но и в реализации других алгоритмов,
например, алгоритмов основанных на методе фрагментальной
дискретизации [1]. ХЕШ-ТАБЛИЦЫ
ДЛЯ ГРАНИЧНЫХ ЭЛЕМЕНТОВ Чтобы построить
хеш-таблицу для граничных элементов, необходимо рассмотреть задачу поиска
пересечений граничных элементов и луча геометрически. Утверждение. Если для вершин плоского
многоугольника выполняются неравенства (4), то они выполняются для всех точек
данного многоугольника. Доказательство. Пусть неравенства (4) выполняются
для вершин многоугольника Без ограничения общности
можно предположить, что Аналогичные рассуждения
применимы и для остальных случаев, когда для точек многоугольника Из данного утверждения следует: 1. Если для узлов гранично-элементной сетки
выполняются неравенства (4), то для любой точки гранично-элементной сетки, тоже
будет выполняться данное неравенство. 2. Для того,
чтобы геометрический объект пересекался с граничным элементом, необходимо,
чтобы существовали точки геометрического объекта, для которых выполнялись следующие
неравенства: где В качестве доказательства первого следствия достаточно рассмотреть сетку
как набор граничных элементов: так как для всех граничных элементов выполнимы
неравенства (4), то они выполнимы и для всей сетки в целом. Тривиально доказательство
второго следствия: так как геометрический объект пересекается с граничным элементом,
то они будут иметь хотя бы одну общую точку, для которой будут выполняться
неравенства (9). Таким образом, гранично-элементная
сетка заключена в параллелепипед (4), заданный минимальными и максимальными
значениями координат узлов сетки. Полученный параллелепипед разбивается на заданные
неравенствами (5) равные части (рис. 2), которым задается индексация согласно (6). Используя неравенства (4),
(5) и функцию (6) можно получить индексы множеств, которым принадлежат точки граничного
элемента: где Из второго следствия очевидно, что поиск пересечений геометрического
объекта с граничным элементом имеет смысл только когда существуют точки
геометрического объекта, для которых выполнимы неравенства (10), где в качестве
параметров Следовательно, при
построении хеш-таблицы для граничных элементов необходимо: 1) найти минимальные и
максимальные координаты узлов сетки; 2) для всех i, j, k удовлетворяющих уравнениям (10) вычислить по формуле
(6) индексы ячеек хеш-таблицы и поместить в данные ячейки соответствующий
граничный элемент; Как и для узлов сетки,
ячейки хеш-таблицы представляют собой открытый массив или список. Обычно на
практике в хеш-таблице хранятся ссылки на граничные элементы, что сокращает
занимаемый объем памяти. В алгоритме
метода композиций необходим поиск граничных элементов пересекающихся с лучом (3).
Для данного случая заполнение хеш-таблицы осуществляется по формулам (10), а
для поиска используются следующие формулы: Формулы (11) получены из
формул (3) и (10), где Информация, хранимая в
построенной хеш-таблице избыточна, но это компенсируется возможностью для любого
геометрического объекта весьма быстро отбросить существенное количество не
нужных граничных элементов и выделить только те, которые могут пересекаться. ЗАКЛЮЧЕНИЕ Рассмотренные хеш-таблицы
для узлов и граничных элементов весьма эффективно применять не только в
реализации метода композиций [2], но и в алгоритмах фрагментальной
дискретизации и разбиений граничных элементов [1], что позволяет существенно сократить
счетное время построения гранично-элементных сеток. Основным преимуществом
данных хеш-таблиц заключается в том, что полный перебор всех элементов
осуществляется только один раз во время заполнения, а при поиске большая часть
элементов не затрагивается. СПИСОК
ЛИТЕРАТУРЫ 1.
Алейников С. М., Вахтин А. А., Тюкачев Н. А. Алгоритмы построения пространственных гранично-элементных
сеток. // Мат. рег. науч.-мет. конф. Информатика:
проблемы, методология, технологии. – Воронеж: ВГУ, 2004. – Вып.
4. – С. 9 – 11. 2.
Вахтин А. А. Метод композиций для гранично-элементной
дискретизации. // Науч.-техн.
Журнал Системы управления и информационные технологии. – Воронеж: Научная
книга, 2005. – № 4 (21) – С. 66 – 71. 3.
Ниман Т. Сортировка и поиск: Рецептурный справочник: Пер. с англ. – М.: Мир,
1998. – 50 с. 4.
Роджерс Д., Адамс Дж.
Математические основы машинной графики: пер. с англ. –
М.: Мир, 2001. – 604 с. 5.
Хаусдорф Ф. Теория множеств: пер. с нем.
– М.: УРСС, 2004. – 304 с. |
| Назад |
Материалы, опубликованные в данном сайте являются авторской интеллектуальной собственностью
и не могут быть использованы ни в каких целях и в никакой форме без письменного разрешения автора
 , где
, где 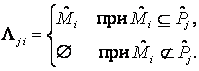
 .
.